DGaussianWavelet
表示导数阶数为 2 的高斯小波的导数.
表示导数阶数为 n 的高斯小波的导数.
更多信息
- DGaussianWavelet 定义了一个非正交小波群.
- 小波函数 (
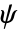 ) 由
) 由 ![((-1)^(n+1))/(sqrt(TemplateBox[{{n, +, {1, /, 2}}}, Gamma])) (partial^n)/(partialx^n)exp(-(x^2)/2) ((-1)^(n+1))/(sqrt(TemplateBox[{{n, +, {1, /, 2}}}, Gamma])) (partial^n)/(partialx^n)exp(-(x^2)/2)](Files/DGaussianWavelet.zh/2.png) 给出.
给出. - DGaussianWavelet 可以用于函数诸如 ContinuousWaveletTransform、WaveletPsi 等.
范例
打开所有单元关闭所有单元范围 (2)
DGaussianWavelet 可以用来执行 ContinuousWaveletTransform:
使用 WaveletScalogram 来获取小波系数的时间尺度表示:
使用 InverseWaveletTransform 来重建信号:
属性和关系 (4)
Wolfram Research (2010),DGaussianWavelet,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DGaussianWavelet.html.
文本
Wolfram Research (2010),DGaussianWavelet,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DGaussianWavelet.html.
CMS
Wolfram 语言. 2010. "DGaussianWavelet." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/DGaussianWavelet.html.
APA
Wolfram 语言. (2010). DGaussianWavelet. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DGaussianWavelet.html 年