DiffusionPDETerm

DiffusionPDETerm[vars]

represents a diffusion term with model variables vars.

DiffusionPDETerm[vars,c]

represents a diffusion term with diffusion coefficient .

DiffusionPDETerm[vars,c,pars]

uses model parameters pars.

Details

  • Diffusion is a central concept of physics that is used in a number of domains, such as thermodynamics, acoustics, structural mechanics and fluid dynamics.
  • Diffusion is also known as conduction.
  • Diffusion with a diffusion coefficient 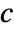is the process of equilibration solely driven by a gradient of the dependent variable :
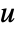  • DiffusionPDETerm returns a differential operators term to be used as a part of partial differential equations:
  • DiffusionPDETerm can be used to model diffusion equations with dependent variable 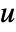, independent variables 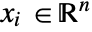and time variable .
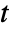  • Stationary model variables vars are vars={u[x1,…,xn],{x1,…,xn}}.
  • Time-dependent model variables vars are vars={u[t,x1,…,xn],{x1,…,xn}} or vars={u[t,x1,…,xn],t,{x1,…,xn}}.
  • The diffusion term 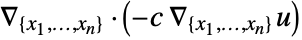in context with other PDE terms is given by:
  • During diffusion, the medium in which the diffusion happens remains stationary, in contrast to convection where the medium is the transport mechanism.
  • The diffusion coefficient 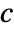can have the following forms:
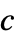
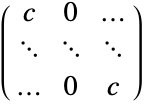
  • cscalar 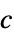, isotropic diffusion
    {c1,…,cn}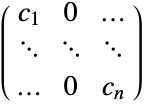
  • vector 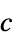, orthotropic diffusion
    • {{c11,…,c1n},…,{cn1,…,cnn}}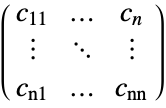
  • matrix 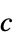, anistropic diffusion
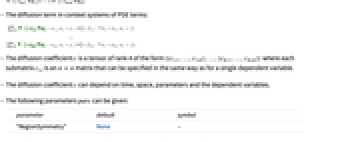
  • For a system of PDEs with dependent variables {u1,…,um}, the diffusion represents:
  • The diffusion term in context systems of PDE terms:
  • The diffusion coefficient 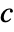is a tensor of rank 4 of the form 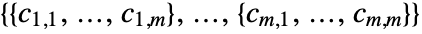where each submatrix 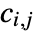is an matrix that can be specified in the same way as for a single dependent variable.
  • The diffusion coefficient can depend on time, space, parameters and the dependent variables.
  • The following parameters pars can be given:
  • parameterdefaultsymbol
    "RegionSymmetry"None
  • A possible choice for the parameter "RegionSymmetry" is "Axisymmetric".
  • "Axisymmetric" region symmetry represents a truncated cylindrical coordinate system where the cylindrical coordinates are reduced by removing the angle variable as follows:
  • dimensionreductionequation
    1D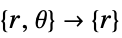
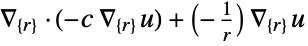
    2D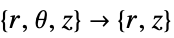
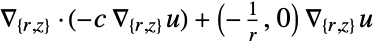
  • The coefficient 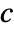affects the meaning of NeumannValue.
  • All quantities that do not explicitly depend on the independent variables given are taken to have zero partial derivative.

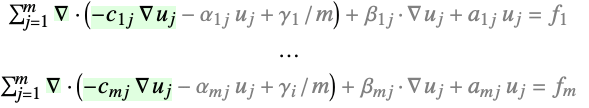
Examples

open allclose all

Basic Examples  (6)

Define a stationary diffusion term:

Activate the term:

Define a stationary diffusion term with a parametric diffusion coefficient replaced:

Activate the term:

Define a symbolic diffusion term:

Activate the term:

Find the eigenvalues of a diffusion term:

Construct a Poisson equation from basic terms and solve it symbolically:

Solve a time-dependent diffusion equation with a Gaussian initial condition:

Visualize the smoothing of the initial condition through time:

Check that the area under the curves remains constant:

Scope  (31)

1D  (6)

Define a symbolic diffusion term:

Not specifying a diffusion coefficient will result in an identity matrix coefficient:

Define a time-dependent diffusion term:

Activate the term:

Define a stationary diffusion term with a parametric diffusion coefficient replaced:

Activate the term:

Use DiffusionPDETerm for modeling an eigenvalue problem:

Use DiffusionPDETerm to set up a 1D Poisson equation:

Visualize the result:

1D Axisymmetric  (1)

Set up a 1D axisymmetric diffusion equation:

Apply Activate to the term:

Verify that the axisymmetric case is a consequence of using a truncated cylindrical coordinate system using the operators that compose the diffusion equation:

2D  (12)

Define a 2D stationary diffusion term:

Activate the term:

Set up a 2D stationary diffusion equation:

Activate the term:

Set up a 2D time-dependent diffusion equation:

Activate the term:

Not specifying a diffusion coefficient will result in an identity matrix coefficient:

Define a 2D orthotropic stationary diffusion term with a vector diffusion coefficient:

Define a 2D stationary diffusion term with an anisotropic diffusion matrix:

Define a 2D diffusion term with an anisotropic diffusion matrix:

Use DiffusionPDETerm to set up a 2D Poisson equation:

Visualize the result:

Construct a Poisson equation from basic PDE terms and solve it numerically:

Visualize the result:

Use a vector-valued diffusion coefficient that has a larger diffusion constant in the direction than the direction:

Visualize the result:

Use a vector-valued diffusion coefficient that has a larger diffusion constant in the direction than the direction:

Visualize the result:

Use an anisotropic diffusion coefficient:

Visualize the result:

2D Axisymmetric  (3)

Set up a 2D axisymmetric diffusion equation:

Apply Activate to the term:

Verify that the axisymmetric case is a consequence of using a truncated cylindrical coordinate system using the operators that compose the diffusion equation:

Set up a 2D axisymmetric diffusion equation:

Apply Activate to the term:

Set up a 2D axisymmetric time-dependent diffusion equation:

Apply Activate to the term:

3D  (1)

Use DiffusionPDETerm to set up a 3D Poisson equation:

Visualize the result:

Coupled  (5)

Define a diffusion term with multiple dependent variables:

Define a diffusion term with multiple dependent variables and multiple diffusion coefficients:

Define a diffusion term with multiple dependent variables and anisotropic diffusion coefficients:

Define a diffusion term with multiple dependent variables and all coefficients specified:

Off-diagonal diffusion coefficients are possible in coupled PDEs:

Solve the equations:

Visualize the results:

Coupled Axisymmetric  (3)

Use DiffusionPDETerm to set up a 1D axisymmetric equation with multiple dependent variables:

Specify boundary conditions:

Solve the equations numerically:

Solve the same equation symbolically:

Visualize the difference between the results:

Define an axisymmetric diffusion term with multiple dependent variables:

Apply Activate to the term:

Define a 2D diffusion axisymmetric term with multiple dependent variables and multiple diffusion coefficients:

Solve the coupled PDEs:

Visualize the results:

Applications  (9)

Use DiffusionPDETerm with a variable diffusion coefficient:

Solve the equation:

Compute the flux:

Visualize the result:

Use DiffusionPDETerm to model conductive heat transfer using an axisymmetric geometry.

The region of analysis is a 2D region. Instead of defining the full 2D region in Cartesian coordinates , you can define a region with truncated cylindrical coordinates in 1D . The cylindrical coordinate variables and vanish because the system is rotationally symmetric around the axis.

Set up the equation:

Specify boundary conditions:

Solve the equation:

Or solve it symbolically with DSolveValue:

Visualize the difference between the results:

Use DiffusionPDETerm to model species diffusion under a dam. Set up the region:

Set up the model:

Solve the equation:

Compute the flux:

Visualize the result:

Find the concentration of species under the dam. Construct the model:

Solve the equation:

Visualize the species concentration:

Define a Helmholtz model:

Solve for the eigenvalues of the Helmholtz equation:

Solve the Helmholtz equation with a source term:

Visualize the solution:

Use DiffusionPDETerm to model conductive heat transfer using an axisymmetric geometry. The region of analysis is a 3D hollow cylinder. Instead of defining the full 3D region in Cartesian coordinates , you can define a region with truncated cylindrical coordinates in 2D . The cylindrical coordinate variable vanishes because the system is rotationally symmetric around the axis.

Set up the region:

Set up the PDE model:

Solve the axisymmetric equation:

Visualize the result:

Visualize the result in 3D space for part of the cylinder:

Use DiffusionPDETerm to model a nonlinear conductive heat transfer using an axisymmetric geometry.

Set up the region:

Find the thermal conductivity for air:

Set up the PDE model:

Solve the equation and measure the time and memory needed to do so:

Visualize the axisymmetric result:

Print the total time to do the computation and number of megabytes used during the evaluation:

Use DiffusionPDETerm to set up a plane stress operator. Set up the coupled coefficients:

Set up the model:

Set up a region:

Solve the equations:

Visualize the results:

Compute the flux:

Define a Stokes-flow model:

Set up the equation:

Define a narrowing region:

Set up a boundary condition:

Solve the equation:

Visualize the solution:

Extend a Stokes-flow model to a Navier–Stokes-flow model. Define a Stokes-flow model:

Define a Navier–Stokes-flow model:

Set up the equation:

Define a region:

Set up a boundary condition:

Solve the equation:

Visualize the solution:

Properties & Relations  (3)

Verify that anisotropic diffusion is the same as :

Visualize that there is no difference in the two solutions:

Solve a time-dependent diffusion equation with a Gaussian initial condition:

The analytical solution is an infinite series:

Extract a few terms from the Inactive sum:

Visualize the difference between the numerical and the analytical solutions:

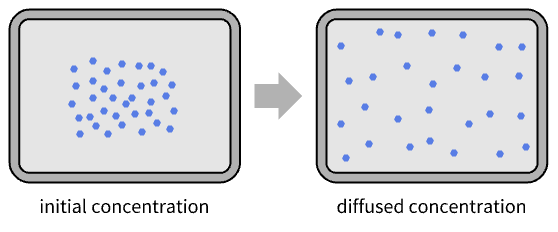
The equilibration property of the diffusion term manifests itself in the smoothing of a discontinuous initial condition:

Visualize the discontinuous initial condition and the smoothed evolution of the initial condition:

Possible Issues  (5)

The negative sign in the operator does not need to be given:

A symbolic diffusion coefficient is interpreted as a matrix diffusion coefficient:

A subsequent substitution must account for that:

An alternative is to specify the symbolic diffusion coefficient as a matrix:

A numeric diffusion coefficient will automatically be multiplied with an IdentityMatrix of proper dimensions:

While solving the differential equation with a scalar diffusion coefficient has been made to work for convenience, subsequent operations may rely on a proper setup:

Solve the equation:

Note that the result tries to take the dot product of a scalar with the gradient of the solution:

Visualizing the result does not work:

One alternative is to directly specify the diffusion coefficient. In the case of a number, the diffusion coefficient is multiplied with the IdentityMatrix:

Solve the equation:

Compute the flux:

Visualize the result:

Yet another alternative is to specify the substituted value as a matrix of dimensions of the number of independent variables:

DiffusionPDETerm models , not :

Visualize the difference in the solutions:

Wolfram Research (2020), DiffusionPDETerm, Wolfram Language function, https://reference.wolfram.com/language/ref/DiffusionPDETerm.html (updated 2022).

Text

Wolfram Research (2020), DiffusionPDETerm, Wolfram Language function, https://reference.wolfram.com/language/ref/DiffusionPDETerm.html (updated 2022).

CMS

Wolfram Language. 2020. "DiffusionPDETerm." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/DiffusionPDETerm.html.

APA

Wolfram Language. (2020). DiffusionPDETerm. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiffusionPDETerm.html

BibTeX

@misc{reference.wolfram_2025_diffusionpdeterm, author="Wolfram Research", title="{DiffusionPDETerm}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/DiffusionPDETerm.html}", note=[Accessed: 22-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_diffusionpdeterm, organization={Wolfram Research}, title={DiffusionPDETerm}, year={2022}, url={https://reference.wolfram.com/language/ref/DiffusionPDETerm.html}, note=[Accessed: 22-February-2025 ]}