DiffusionPDETerm

DiffusionPDETerm[vars]

表示模型变量为 vars 的扩散项 .

DiffusionPDETerm[vars,c]

表示扩散系数为 的扩散项 .

DiffusionPDETerm[vars,c,pars]

使用模型参数 pars.

更多信息

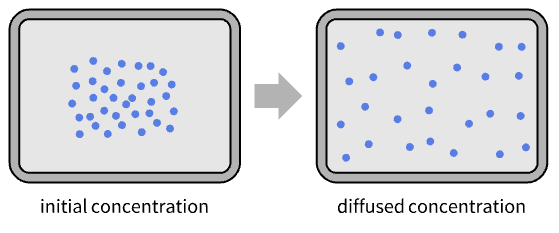
  • 扩散是物理学的中心概念，应用于许多领域，如热力学、声学、结构力学和流体动力学等.
  • 扩散也称为传导（Conduction）.
  • 扩散系数为 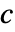的扩散是仅由因变量 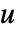的梯度驱动的平衡过程：
  • DiffusionPDETerm 返回微分算子项，该项将用作偏微分方程的一部分：
  • DiffusionPDETerm 可用来模拟扩散方程，其中因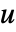变量为 ，自变量为 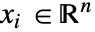，时间变量为 .
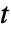  • 平稳模型变量 vars 为 vars={u[x1,…,xn],{x1,…,xn}}.
  • 与时间相关的模型变量 vars 为 vars={u[t,x1,…,xn],{x1,…,xn}} 或 vars={u[t,x1,…,xn],t,{x1,…,xn}}.
  • 与其他偏微分方程项相关的扩散项 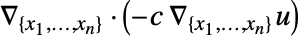由下式给出：
  • 在扩散过程中，发生扩散的介质保持静止，这与介质作为输送机制的对流相反.
  • 扩散系数 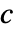具有以下形式：
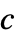
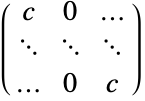
  • c标量 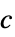，各向同性扩散
    {c1,…,cn}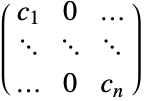
  • 向量 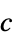，正交各向异性扩散
    • {{c11,…,c1n},…,{cn1,…,cnn}}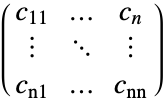
  • 矩阵 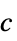，各向异性扩散
  • 对于具有因变量 {u1,…,um} 的偏微分方程组，扩散表示：
  • 扩散项在相关的偏微分方程组中：
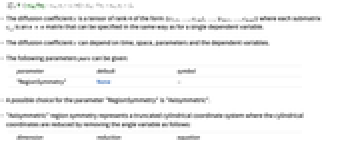
  • 扩散系数 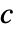是秩为 4 的张量，形如 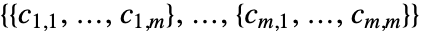，其中各子矩阵 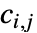为 矩阵，其指定方式与单个因变量的指定方式相同.
  • 扩散系数 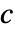可取决于时间、空间、参数和因变量.
  • 可以给出以下参数 pars：
  • 参数默认符号
    "RegionSymmetry"None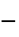
  • 参数 "RegionSymmetry" 的一个可能选择为 "Axisymmetric".
  • "Axisymmetric" 区域对称性表示截断圆柱坐标系，其中通过移除角度变量来简化圆柱坐标，如下所示：
  • 维度简化方程式
    1D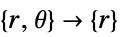
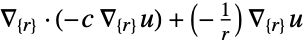
    2D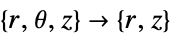
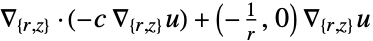
  • 系数 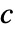影响 NeumannValue 的意义.
  • 所有不明确依赖于给定自变量的量，其偏导数均被视为零.

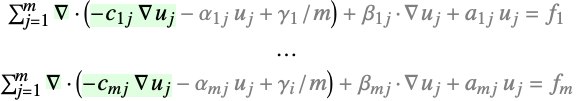
范例

打开所有单元关闭所有单元

基本范例  (6)

定义平稳扩散项：

激活该项：

定义一个平稳扩散项，并用参数扩散系数替换：

激活该项：

定义符号扩散项：

激活该项：

求扩散项的特征值：

从基本的项构造一个泊松方程，并进行符号求解：

求解与时间有关并具有高斯初始条件的扩散方程：

可视化初始条件随时间的平滑：

查看曲线下的面积是否保持不变：

范围  (31)

一维  (6)

定义符号扩散项：

不指定扩散系数将产生单位矩阵系数：

定义与时间相关的扩散项：

激活该项：

定义一个用参数扩散系数替换的固定扩散项：

激活该项：

使用 DiffusionPDETerm 模拟特征值问题：

使用 DiffusionPDETerm 建立一维泊松方程：

可视化结果：

一维轴对称  (1)

建立一维轴对称扩散方程：

将 Activate 应用于该项：

使用构成扩散方程的算子验证轴对称情况是使用截断圆柱坐标系的结果：

二维  (12)

定义二维平稳扩散项：

激活该项：

建立二维平稳扩散方程：

激活该项：

建立与时间相关的二维扩散方程：

激活该项：

不指定扩散系数将导致单位矩阵系数：

使用向量扩散系数定义二维正交各向异性平稳扩散项：

使用各向异性扩散矩阵定义二维平稳扩散项：

使用各向异性扩散矩阵定义二维扩散项：

使用 DiffusionPDETerm 建立二维泊松方程：

可视化结果：

用偏微分方程的基本项构造一个泊松方程，并用数值方法求解：

可视化结果：

使用向量值扩散系数，该系数在 方向的扩散常数大于 方向的扩散常数：

可视化结果：

使用向量值扩散系数，该系数在 方向的扩散常数大于 方向的扩散常数：

可视化结果：

使用各向异性扩散系数：

可视化结果：

二维轴对称  (3)

建立一个二维轴对称扩散方程：

将 Activate 应用于项：

使用构成扩散方程的算子验证轴对称情况是使用截断圆柱坐标系的结果：

建立一个二维轴对称时间相关扩散方程：

将 Activate 应用于项：

建立一个二维轴对称时依扩散方程：

将 Activate 应用于项：

三维  (1)

使用 DiffusionPDETerm 建立三维泊松方程：

可视化结果：

耦合  (5)

定义具有多个因变量的扩散项：

定义具有多个因变量和多个扩散系数的扩散项：

定义具有多个因变量和各向异性扩散系数的扩散项：

定义具有多个因变量和所有指定系数的扩散项：

在耦合 PDE 中可能存在非对角线扩散系数：

求解方程：

可视化结果：

耦合轴对称  (3)

使用 DiffusionPDETerm 建立具有多个因变量的一维轴对称方程：

指定边界条件：

数值求解方程：

符号求解相同的方程：

可视化结果之间的差异：

定义具有多个因变量的轴对称扩散项：

将 Activate 应用于项：

定义具有多个因变量和多个扩散系数的二维扩散轴对称项：

求解耦合偏微分方程：

可视化结果：

应用  (9)

使用带有可变扩散系数的 DiffusionPDETerm：

解方程：

计算通量：

可视化结果：

将 DiffusionPDETerm 用于轴对称几何对传导热传递进行建模中.

分析区域是二维区域. 除了在笛卡尔坐标 中定义完整的二维区域，您还可以在一维 中定义具有截断圆柱坐标的区域. 因为方程组围绕 轴旋转对称因此柱坐标变量 和 消失.

建立方程：

指定边界条件：

解方程：

或用 DSolveValue 符号求解：

可视化结果之间的差异：

使用 DiffusionPDETerm 模拟大坝下的物种扩散. 设置区域：

设置模型：

解方程：

计算通量：

可视化结果：

求大坝下的物种浓度. 构造模型：

解方程：

可视化物种浓度：

定义亥姆霍兹模型：

求解亥姆霍兹方程的特征值：

求解带有源项的亥姆霍兹方程：

可视化解：

将 DiffusionPDETerm 用于轴对称几何对传导热传递进行的建模. 分析区域是一个三维空心圆柱体. 除了在笛卡尔坐标 中定义完整的三维区域，您还可以在二维 中定义具有截断圆柱坐标的区域. 因为方程组围绕 轴旋转对称因此柱坐标变量 消失.

设置区域：

设置 PDE 模型：

求解轴对称方程：

可视化结果：

在三维空间中可视化部分圆柱体的结果：

使用 DiffusionPDETerm 使用轴对称几何对非线性传导热传递进行建模.

设置区域：

求空气的热导率：

设置 PDE 模型：

求解方程并衡量这样做所需的时间和内存：

可视化轴对称结果：

打印计算的总时间和评估期间使用的兆字节数：

使用 DiffusionPDETerm 设置平面应力算子. 设置耦合系数：

设置模型：

设置区域：

解方程：

可视化结果：

计算通量：

定义斯托克斯流模型：

建立方程：

定义一个逐渐缩小的区域：

设置边界条件：

解方程：

可视化解：

将斯托克斯流模型扩展为纳维-斯托克斯流模型. 定义斯托克斯流模型：

定义纳维-斯托克斯流模型：

建立方程：

定义区域：

设置边界条件：

解方程：

可视化解：

属性和关系  (3)

验证各向异性扩散 与 相同：

用视图说明两种解决方案没有区别：

求解高斯初始条件下的与时间有关的扩散方程：

解析解是一个无限级数：

从 Inactive 和中提取几个项：

可视化数值解和解析解之差：

扩散项的平衡特性在不连续初始条件的平滑过程中表现出来：

可视化不连续初始条件和初始条件的平滑演化：

可能存在的问题  (5)

算子 中的负号不需要给出：

符号扩散系数被解释为矩阵扩散系数：

随后的替换必须说明这一点：

另一种方法是将符号扩散系数指定为矩阵：

数值扩散系数将自动乘以适当大小的 IdentityMatrix：

尽管使用标量扩散系数求解微分方程是可行的，但随后的运算取决于正确的设置：

解方程：

请注意，尝试采用标量与解的梯度的点积作为结果：

可视化结果不起作用：

一种替代方法是直接指定扩散系数. 对于数字的情形，扩散系数须乘以 IdentityMatrix：

解方程：

计算通量：

可视化结果：

还有一种方法是将替换值指定为维度为自变量个数的矩阵：

DiffusionPDETerm 模拟 ，而不是 ：

可视化解之间的差异：

Wolfram Research (2020)，DiffusionPDETerm，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DiffusionPDETerm.html （更新于 2022 年）.

文本

Wolfram Research (2020)，DiffusionPDETerm，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DiffusionPDETerm.html （更新于 2022 年）.

CMS

Wolfram 语言. 2020. "DiffusionPDETerm." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/DiffusionPDETerm.html.

APA

Wolfram 语言. (2020). DiffusionPDETerm. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiffusionPDETerm.html 年

BibTeX

@misc{reference.wolfram_2024_diffusionpdeterm, author="Wolfram Research", title="{DiffusionPDETerm}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/DiffusionPDETerm.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_diffusionpdeterm, organization={Wolfram Research}, title={DiffusionPDETerm}, year={2022}, url={https://reference.wolfram.com/language/ref/DiffusionPDETerm.html}, note=[Accessed: 05-November-2024 ]}