DirichletTransform[expr,n,s]
gives the Dirichlet transform of expr with respect to n.


DirichletTransform
DirichletTransform[expr,n,s]
gives the Dirichlet transform of expr with respect to n.
Details and Options
- The Dirichlet transform for a discrete function
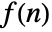 is given by
is given by 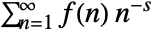 .
. - The following options can be given:
-
Assumptions $Assumptions assumptions to make about parameters GenerateConditions False whether to generate answers that involve conditions on parameters Method Automatic method to use VerifyConvergence True whether to verify convergence
Examples
open all close allOptions (1)
GenerateConditions (1)
Set GenerateConditions to True to get the region of convergence:
Related Guides
History
Text
Wolfram Research (2008), DirichletTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/DirichletTransform.html.
CMS
Wolfram Language. 2008. "DirichletTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DirichletTransform.html.
APA
Wolfram Language. (2008). DirichletTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DirichletTransform.html
BibTeX
@misc{reference.wolfram_2025_dirichlettransform, author="Wolfram Research", title="{DirichletTransform}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/DirichletTransform.html}", note=[Accessed: 28-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_dirichlettransform, organization={Wolfram Research}, title={DirichletTransform}, year={2008}, url={https://reference.wolfram.com/language/ref/DirichletTransform.html}, note=[Accessed: 28-January-2026]}