DiscreteRiccatiSolve
DiscreteRiccatiSolve[{a,b},{q,r}]
给出矩阵 ![]() ,它是离散代数 Riccati 方程
,它是离散代数 Riccati 方程 ![]() 的稳定解.
的稳定解.
DiscreteRiccatiSolve[{a,b},{q,r,p}]
求解 ![]() .
.
更多信息和选项

- 在
![TemplateBox[{a}, ConjugateTranspose].x.a-x-TemplateBox[{a}, ConjugateTranspose].x.b.TemplateBox[{{(, {r, +, {TemplateBox[{b}, ConjugateTranspose], ., x, ., b}}, )}}, Inverse].TemplateBox[{b}, ConjugateTranspose].x.a+q=0 TemplateBox[{a}, ConjugateTranspose].x.a-x-TemplateBox[{a}, ConjugateTranspose].x.b.TemplateBox[{{(, {r, +, {TemplateBox[{b}, ConjugateTranspose], ., x, ., b}}, )}}, Inverse].TemplateBox[{b}, ConjugateTranspose].x.a+q=0](Files/DiscreteRiccatiSolve.zh/4.png) 中,
中,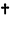 表示共轭转置.
表示共轭转置. - 仅当
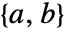 稳定、
稳定、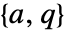 可测、
可测、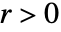 且
且 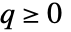 时,方程
时,方程 ![TemplateBox[{a}, ConjugateTranspose].x.a-x-TemplateBox[{a}, ConjugateTranspose].x.b.TemplateBox[{{(, {r, +, {TemplateBox[{b}, ConjugateTranspose], ., x, ., b}}, )}}, Inverse].TemplateBox[{b}, ConjugateTranspose].x.a+q=0 TemplateBox[{a}, ConjugateTranspose].x.a-x-TemplateBox[{a}, ConjugateTranspose].x.b.TemplateBox[{{(, {r, +, {TemplateBox[{b}, ConjugateTranspose], ., x, ., b}}, )}}, Inverse].TemplateBox[{b}, ConjugateTranspose].x.a+q=0](Files/DiscreteRiccatiSolve.zh/10.png) 有唯一对称的正半定解. 因此,矩阵
有唯一对称的正半定解. 因此,矩阵 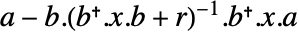 的所有特征值位于单位圆内,并且解是稳定的.
的所有特征值位于单位圆内,并且解是稳定的. - 当
 可控且
可控且  可观测时,解是正定的.
可观测时,解是正定的. - DiscreteRiccatiSolve 支持 Method 选项. 可以指定以下选项:
-
Automatic 自动确定方法 "Eigensystem" 基于特征分解 "GeneralizedEigensystem" 基于广义特征分解 "GeneralizedSchur" 基于广义舒尔分解 "InverseFree" "GeneralizedSchur" 的变型 "MatrixSign" - 使用矩阵符号函数的迭代法
"Newton" 迭代牛顿法 "Schur" 基于舒尔分解 - 所有方法适用于近似数值矩阵. "Eigensystem" 适用于精确矩阵.
范例
打开所有单元关闭所有单元选项 (7)
Method (7)
应用 (2)
属性和关系 (11)
DiscreteRiccatiSolve[{a,b},{q,r,p}] 等价于 DiscreteRiccatiSolve[{a-b.![]() .p,b},{q-p.r -1.p,r}]:
.p,b},{q-p.r -1.p,r}]:
如果 {a,b} 是稳定的,{a,g} 可检测,且 q=Transpose[g].g,则离散 Riccati 方程的解是半正定的:
如果 {a,b} 可控制,{a,g} 可观测,且 q=Transpose[g].g,则离散 Riccati 方程的解是正定的:
辛矩阵必须满足稳定性和互补性,以获得 Riccati 方程的稳定解:
使用 DiscreteRiccatiSolve 计算最优状态反馈增益:
使用 LQRegulatorGains 直接获得相同结果:
使用 DiscreteRiccatiSolve 计算最优输出反馈增益:
LQOutputRegulatorGains 给出相同结果:
使用 DiscreteRiccatiSolve 计算最优估计器增益:
使用 LQEstimatorGains:
文本
Wolfram Research (2010),DiscreteRiccatiSolve,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteRiccatiSolve.html (更新于 2014 年).
CMS
Wolfram 语言. 2010. "DiscreteRiccatiSolve." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/DiscreteRiccatiSolve.html.
APA
Wolfram 语言. (2010). DiscreteRiccatiSolve. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiscreteRiccatiSolve.html 年