WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

DispersionEstimatorFunction

一般化された線形モデルフィット関数のオプションで，分散パラメータの推定法を指定する．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
関連項目
関連するガイド
履歴
引用書式

DispersionEstimatorFunction

DispersionEstimatorFunction

一般化された線形モデルフィット関数のオプションで，分散パラメータの推定法を指定する．

詳細

  • DispersionEstimatorFunctionは，GeneralizedLinearModelFit，LogitModelFit，ProbitModelFitのオプションである．
  • DispersionEstimatorFunction->"PearsonChiSquare"とすると，推定法は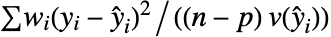となる．ただし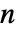， はデータ点の数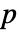， はパラメータの数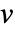， は分布の分散関数である．
  • DispersionEstimatorFunction->Automaticとすると，次の推定法が使われる．
  • "Binomial"1
    "Gamma"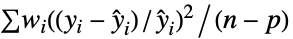
    "Gaussian"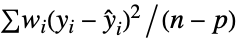
    "InverseGaussian"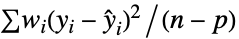
    "Poisson"1
    "QuasiLikelihood"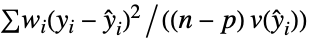
  • デフォルトではない値を使って"Binomial"および"Poisson"モデルにおける過分散のモデル化を行うことができる．
  • DispersionEstimatorFunction->f と設定すると，一般的な分散は f[y,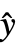,w]で推定される．ただし，y={y1,y2,…}は観察値のリスト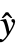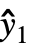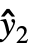，={,,…}は予測値のリスト，w={w1,w2,…}は測度 yiの重みのリストである．

例題

すべて開く すべて閉じる

例  (1)

ポアソン(Poisson)モデルをフィットする：

デフォルトの分散推定を使って共分散行列を構築する：

ピアソン(Pearson)の で分散を推定する：

平均平方誤差で分散を推定する：

スコープ  (2)

FittedModel内で推定を定義する：

ロジットモデルをフィットする：

誤差の平方の和で分散を推定する：

プロビットモデルをフィットする：

平均平方誤差で分散を推定する：

Wolfram Research (2008), DispersionEstimatorFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/DispersionEstimatorFunction.html.

テキスト

Wolfram Research (2008), DispersionEstimatorFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/DispersionEstimatorFunction.html.

CMS

Wolfram Language. 2008. "DispersionEstimatorFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DispersionEstimatorFunction.html.

APA

Wolfram Language. (2008). DispersionEstimatorFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DispersionEstimatorFunction.html

BibTeX

@misc{reference.wolfram_2025_dispersionestimatorfunction, author="Wolfram Research", title="{DispersionEstimatorFunction}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/DispersionEstimatorFunction.html}", note=[Accessed: 18-September-2025]}

BibLaTeX

@online{reference.wolfram_2025_dispersionestimatorfunction, organization={Wolfram Research}, title={DispersionEstimatorFunction}, year={2008}, url={https://reference.wolfram.com/language/ref/DispersionEstimatorFunction.html}, note=[Accessed: 18-September-2025]}