LogitModelFit

LogitModelFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]

constructs a binomial logistic regression model of the form that fits the yi for each xi.

LogitModelFit[data,{f1,…},{x1,x2,…}]

constructs a binomial logistic regression model of the form where the fi depend on the variables xk.

LogitModelFit[{m,v}]

constructs a binomial logistic regression model from the design matrix m and response vector v.

Details and Options

  • LogitModelFit attempts to model the data using a linear combination of basis functions composed with a logistic sigmoid.
  • LogitModelFit is typically used in classification to model probability values.
  • LogitModelFit produces a generalized linear model of the form 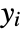under the assumption that the original 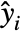are independent realizations of Bernoulli trials with probabilities .
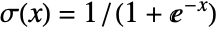  • The function 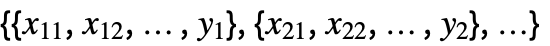is the LogisticSigmoid.
  • LogitModelFit returns a symbolic FittedModel object to represent the logistic model it constructs. The properties and diagnostics of the model can be obtained from model["property"].
  • The value of the best-fit function from LogitModelFit at a particular point x1, … can be found from model[x1,…].
  • Possible forms of data are:
  • {y1,y2,…}equivalent to the form {{1,y1},{2,y2},…}
    {{x11,x12,…,y1},…}a list of independent values xij and the responses yi
    {{x11,x12,…}y1,…}a list of rules between input values and responses
    {{x11,x12,…},…}{y1,y2,…}a rule between a list of input values and responses
    {{x11,…,y1,…},…}nfit the n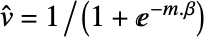th column of a matrix
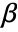  • With multivariate data such as {{x_(11),x_(12),... ,y_(1)},{x_(21),x_(22),... ,y_(2)},...}, the number of coordinates xi1, xi2, … should equal the number of variables xi.
  • The yi are probabilities between 0 and 1.
  • Additionally, data can be specified using a design matrix without specifying functions and variables:
  • {m,v}a design matrix m and response vector v
  • In LogitModelFit[{m,v}], the design matrix m is formed from the values of basis functions fi at data points in the form {{f1,f2,…},{f1,f2,…},…}. The response vector v is the list of responses {y1,y2,…}.
  • For a design matrix m and response vector v, the model is 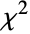, where 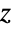is the vector of parameters to be estimated.
  • When a design matrix is used, the basis functions fi can be specified using the form LogitModelFit[{m,v},{f1,f2,…}].
  • LogitModelFit is equivalent to GeneralizedLinearModelFit with ExponentialFamily->"Binomial" and LinkFunction->Automatic.
  • LogitModelFit takes the same options as GeneralizedLinearModelFit, with the exception of ExponentialFamily and LinkFunction.

Examples

open allclose all

Basic Examples  (1)

Define a dataset:

Fit a logistic model to the data:

Evaluate the model at a point:

Plot the data points and the models:

Scope  (13)

Data  (6)

Fit data with success probability responses, assuming increasing integer-independent values:

This is equivalent to:

Weight by the number of observations for each predictor value:

This gives the same best fit function as success failure data:

Fit a list of rules:

Fit a rule of input values and responses:

Specify a column as the response:

Fit a model given a design matrix and response vector:

See the functional form:

Fit the model referring to the basis functions as x and y:

Obtain a list of available properties:

Properties  (7)

Data & Fitted Functions  (1)

Fit a logit model:

Extract the original data:

Obtain and plot the best fit:

Obtain the fitted function as a pure function:

Get the design matrix and response vector for the fitting:

Residuals  (1)

Examine residuals for a fit:

Visualize the raw residuals:

Visualize Anscombe residuals and standardized Pearson residuals in stem plots:

Dispersion and Deviances  (1)

Fit a logit model to some data:

The estimated dispersion is 1 by default:

Use Pearson's as the dispersion estimator instead:

Plot the deviances for each point:

Obtain the analysis of deviance table:

Get the residual deviances from the table:

Parameter Estimation Diagnostics  (1)

Obtain a formatted table of parameter information:

Extract the column of -statistic values:

Influence Measures  (1)

Fit some data containing extreme values to a logit model:

Check Cook distances to identify highly influential points:

Check the diagonal elements of the hat matrix to assess influence of points on the fitting:

Prediction Values  (1)

Fit a logit model:

Plot the predicted values against the observed values:

Goodness-of-Fit Measures  (1)

Obtain a table of goodness-of-fit measures for a logit model:

Compute goodness-of-fit measures for all subsets of predictor variables:

Rank the models by AIC:

Generalizations & Extensions  (1)

Perform other mathematical operations on the functional form of the model:

Integrate symbolically and numerically:

Find a predictor value that gives a particular value for the model:

Options  (8)

ConfidenceLevel  (1)

The default gives 95% confidence intervals:

Use 99% intervals instead:

Set the level to 90% within FittedModel:

CovarianceEstimatorFunction  (1)

Fit a logit model:

Compute the covariance matrix using the expected information matrix:

Use the observed information matrix instead:

DispersionEstimatorFunction  (1)

Fit a logit model:

Compute the covariance matrix:

Compute the covariance matrix estimating the dispersion by Pearson's :

IncludeConstantBasis  (1)

Fit a logit model:

Fit the model with no constant term:

LinearOffsetFunction  (1)

Fit data to a logit model:

Fit data to a model with a known Sqrt[x] term:

NominalVariables  (1)

Fit the data treating the first variable as a nominal variable:

Treat both variables as nominal:

Weights  (1)

Fit a model using equal weights:

Give explicit weights for the data points:

WorkingPrecision  (1)

Use WorkingPrecision to get higher precision in parameter estimates:

Obtain the fitted function:

Reduce the precision in property computations after the fitting:

Properties & Relations  (4)

A default "Binomial" model from GeneralizedLinearModelFit is equivalent to the model for LogitModelFit:

ProbitModelFit is equivalent to a "Binomial" model with "ProbitLink":

LogitModelFit assumes binomially distributed responses:

NonlinearModelFit assumes normally distributed responses:

The fits are not identical:

LogitModelFit will use the time stamps of a TimeSeries as variables:

Rescale the time stamps and fit again:

Find fit for the values:

LogitModelFit acts pathwise on a multipath TemporalData:

Possible Issues  (1)

Responses outside the interval from 0 to 1 are not valid for logit models:

Wolfram Research (2008), LogitModelFit, Wolfram Language function, https://reference.wolfram.com/language/ref/LogitModelFit.html.

Text

Wolfram Research (2008), LogitModelFit, Wolfram Language function, https://reference.wolfram.com/language/ref/LogitModelFit.html.

CMS

Wolfram Language. 2008. "LogitModelFit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LogitModelFit.html.

APA

Wolfram Language. (2008). LogitModelFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LogitModelFit.html

BibTeX

@misc{reference.wolfram_2024_logitmodelfit, author="Wolfram Research", title="{LogitModelFit}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/LogitModelFit.html}", note=[Accessed: 26-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_logitmodelfit, organization={Wolfram Research}, title={LogitModelFit}, year={2008}, url={https://reference.wolfram.com/language/ref/LogitModelFit.html}, note=[Accessed: 26-December-2024 ]}