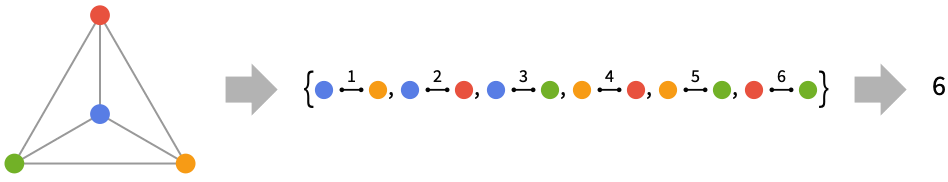WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

EdgeCount
✖
EdgeCount

✖

gives a count of the number of edges in the graph g.

✖
EdgeCount[g,patt]

gives a count of the number of edges that match the pattern patt.

✖
EdgeCount[{vw,…},…]

uses rules vw to specify the graph g.

Details

  • EdgeCount is also known as the size of the graph.
  • Multiple edges between nodes are counted as separate.
  • EdgeCount works with undirected graphs, directed graphs, multigraphs and mixed graphs.

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

Count the number of edges:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-b1kkxi
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-b3rg0e
Out[2]=2

Count the number of edges that match a pattern:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-olztr
Out[1]=1

The number of edges incident to 1:

In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-fzbrwl
Out[2]=2

Scope  (7)Survey of the scope of standard use cases

EdgeCount works with undirected graphs:

In[3]:=3
✖
https://wolfram.com/xid/0cg4pc29u-y99orn
Out[3]=3

Directed graphs:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-f3ma9n
Out[1]=1

Multigraphs:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-uvnf7h
Out[1]=1

Mixed graphs:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-5geyu
Out[1]=1

Use rules to specify the graph:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-bndh30
Out[1]=1

Use a pattern to count a subset of edges:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-53nmq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-cszard
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cg4pc29u-cnnizt
Out[3]=3

Works with large graphs:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-pq9ae
In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-lgy7yy
Out[2]=2

Generalizations & Extensions  (1)Generalized and extended use cases

Count the number of edges on symbolic graph constructors:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-kaghv3
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-b77x3e
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cg4pc29u-bxol7n
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0cg4pc29u-dnfq4d
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0cg4pc29u-fre4dl
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0cg4pc29u-ngm30
Out[6]=6
In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-ie64y
Out[1]=1
In[8]:=8
✖
https://wolfram.com/xid/0cg4pc29u-dnjiv
Out[8]=8
In[9]:=9
✖
https://wolfram.com/xid/0cg4pc29u-iymgk
Out[9]=9
In[10]:=10
✖
https://wolfram.com/xid/0cg4pc29u-0kvl6
Out[10]=10
In[11]:=11
✖
https://wolfram.com/xid/0cg4pc29u-kqp2v9
Out[11]=11
In[12]:=12
✖
https://wolfram.com/xid/0cg4pc29u-bzvv78
Out[12]=12

Applications  (2)Sample problems that can be solved with this function

The minimum number of edges in a connected graph with vertices is :

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-bge9sr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-bkwc58
Out[2]=2

A path graph with vertices has exactly edges:

In[3]:=3
✖
https://wolfram.com/xid/0cg4pc29u-iqoccl
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0cg4pc29u-tfe5e
Out[4]=4

The number of edges for Bernoulli graphs with probability on vertices has mean pTemplateBox[{n, 2}, Binomial]:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-lqqrc2
In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-8xqbp
Out[2]=2

The standard deviation is sqrt(p (1-p) TemplateBox[{n, 2}, Binomial]):

In[3]:=3
✖
https://wolfram.com/xid/0cg4pc29u-bgrhnr
Out[3]=3

The full distribution:

In[4]:=4
✖
https://wolfram.com/xid/0cg4pc29u-bz6k12
Out[4]=4

Properties & Relations  (7)Properties of the function, and connections to other functions

The number of edges of CompleteGraph[n]:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-uaq6r
Out[1]=1

EdgeCount can be found using EdgeList:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-rtzao
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-cnrlqt
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cg4pc29u-dw7ac3
Out[3]=3

The number of edges for a directed graph can be found from matrix representations:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-dxrnuc
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-b6qsb8
Out[2]=2

Totaling the adjacency matrix:

In[3]:=3
✖
https://wolfram.com/xid/0cg4pc29u-bci0zk
Out[3]=3

The number of columns of the incidence matrix:

In[4]:=4
✖
https://wolfram.com/xid/0cg4pc29u-h2ry9v
Out[4]=4

The number of edges for an undirected graph can be found from matrix representations:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-dn3kq0
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-0nrde
Out[2]=2

The total of the upper (or lower) triangular part of the adjacency matrix:

In[3]:=3
✖
https://wolfram.com/xid/0cg4pc29u-burep
Out[3]=3

The number of columns of the incidence matrix:

In[4]:=4
✖
https://wolfram.com/xid/0cg4pc29u-l1r5kf
Out[4]=4

Totaling the diagonal elements of the Kirchhoff matrix, divided by 2:

In[5]:=5
✖
https://wolfram.com/xid/0cg4pc29u-c6ou08
Out[5]=5

The number of edges of the graph is equal to the number of vertices of its line graph:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-bv7fow
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-fvjkui
Out[2]=2

The sum of the degrees of all vertices of a graph is twice the number of edges:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-nc90z
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-dga86
Out[2]=2

The underlying undirected graph of a graph g has the same number of edges as g:

In[1]:=1
✖
https://wolfram.com/xid/0cg4pc29u-1sko1
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cg4pc29u-qhgql
Out[2]=2
Wolfram Research (2010), EdgeCount, Wolfram Language function, https://reference.wolfram.com/language/ref/EdgeCount.html (updated 2015).
✖
Wolfram Research (2010), EdgeCount, Wolfram Language function, https://reference.wolfram.com/language/ref/EdgeCount.html (updated 2015).

Text

Wolfram Research (2010), EdgeCount, Wolfram Language function, https://reference.wolfram.com/language/ref/EdgeCount.html (updated 2015).

✖
Wolfram Research (2010), EdgeCount, Wolfram Language function, https://reference.wolfram.com/language/ref/EdgeCount.html (updated 2015).

CMS

Wolfram Language. 2010. "EdgeCount." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/EdgeCount.html.

✖
Wolfram Language. 2010. "EdgeCount." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/EdgeCount.html.

APA

Wolfram Language. (2010). EdgeCount. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EdgeCount.html

✖
Wolfram Language. (2010). EdgeCount. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EdgeCount.html

BibTeX

@misc{reference.wolfram_2025_edgecount, author="Wolfram Research", title="{EdgeCount}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/EdgeCount.html}", note=[Accessed: 08-July-2025 ]}

✖
@misc{reference.wolfram_2025_edgecount, author="Wolfram Research", title="{EdgeCount}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/EdgeCount.html}", note=[Accessed: 08-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_edgecount, organization={Wolfram Research}, title={EdgeCount}, year={2015}, url={https://reference.wolfram.com/language/ref/EdgeCount.html}, note=[Accessed: 08-July-2025 ]}

✖
@online{reference.wolfram_2025_edgecount, organization={Wolfram Research}, title={EdgeCount}, year={2015}, url={https://reference.wolfram.com/language/ref/EdgeCount.html}, note=[Accessed: 08-July-2025 ]}