WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

EdgeCycleMatrix

EdgeCycleMatrix[g]

グラフ g の辺閉路行列を与える．

EdgeCycleMatrix[{vw,…}]

規則 vw を使ってグラフ g を指定する．

詳細

EdgeCycleMatrixは，タイセット行列あるいはループ行列としても知られている．
EdgeCycleMatrixは，各行がグラフ g の閉路 i に，各列が辺 e_jに対応する行列 c_ij を返す．
無向グラフの場合，c_ijは，辺 e_jが閉路 i の一部であるなら1であり，それ以外の場合は0である．
有向グラフの場合，c_ijは，辺 e_jが閉路 i の一部であるなら1，逆方向の辺 e_jが閉路 i の一部であるなら-1，それ以外の場合は0である．
辺 e_jは，EdgeList[g]における位置 j の辺であり，辺 e_jの指標 j はEdgeIndex[g,e_j]で求めることができる．
EdgeCycleMatrixは，グラフ g 中のすべての閉路の基底を与える．
EdgeCycleMatrixは，無向グラフ，有向グラフ，多重グラフ，混合グラフに使うことができる．

予備知識

EdgeCycleMatrixは，各行がグラフの閉路 i に，そして各列が辺 e_jに対応する行列 c_ijを返す．辺閉路行列は，グラフ内の辺と閉路の結合によって決定され，辺閉路行列の閉路は，グラフの閉路の基底を形成する．閉路の基底は，化学グラフを調べる場合，大規模な閉路族を生成する場合，そして回路の電圧や電流を計算するのに便利である．辺閉路行列は，タイセット行列またはループ行列としても知られる．
無向グラフについては，辺 e_jが閉路 i の一部である場合には，c_ijは1であり，その他の場合にはゼロである．有向グラフについては，c_ijは，辺 e_jが閉路 i の一部である場合には1であり，逆方向の辺 e_jが閉路 i の一部である場合には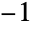であり，それ以外の場合にはゼロである．
FindFundamentalCyclesは，グラフの基本閉路のリストを得るのに使える関連関数である．

例題

すべて開くすべて閉じる

例 (2)

グラフの辺閉路行列を求める：

グラフの閉路基底を得る：

閉路を示す：

スコープ (6)

EdgeCycleMatrixは無向グラフに使うことができる：

有向グラフに使う：

多重グラフ：

混合グラフ：

規則を使ってグラフを指定する：

EdgeCycleMatrixは大きいグラフに使うことができる：

アプリケーション (1)

グラフの閉路基底を得る：

すべての単純閉路を構築する：

特性と関係 (3)

EdgeListを使って閉路表現を得る：

n 個の頂点と m 本の辺のある連結グラフ：

次元(m-n+1)×m の辺閉路行列を持つ：

IncidenceMatrixからEdgeCycleMatrixを計算する：

EdgeCycleMatrixと比較する：

トップへ