Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

EdgeCycleMatrix

EdgeCycleMatrix[g]

给出图 g 的边圈矩阵.

EdgeCycleMatrix[{vw,…}]

用规则 vw 指定图 g.

更多信息

EdgeCycleMatrix 也被称为带集矩阵或循环矩阵.
EdgeCycleMatrix 返回一个矩阵 c_ij，它的每一行对应于图 g 中的一个圈 i 而每一列对应于一条边 e_j.
对无向图，若边 e_j 是圈 i 的组成部分则 c_ij 为 1 否则为零.
对有向图，若边 e_j 是圈 i 的组成部分则 c_ij 为 1，若边 e_j 在反方向上是圈 i 的组成部分则 c_ij 为 -1，其它情况则为零.
边 e_j 是 EdgeList[g] 中在位置 j 上的边，而边 e_j 的下标 j 可以用 EdgeIndex[g,e_j] 求得.
EdgeCycleMatrix 给出了图 g 中所有圈的基.
EdgeCycleMatrix 适用于无向图、有向图、多重图和混合图.

背景

EdgeCycleMatrix 返回一个矩阵 c_ij，它的每一行对应于图中的一个圈 i 而每一列对应于一条边 e_j. 边圈矩阵由图中边和圈的关联决定，而且边圈矩阵中的圈形成了图的圈基. 圈基对研究化学图，生成大的圈族，以及计算电路的电压和电流都非常有用. 边圈矩阵也被称为带集矩阵或循环矩阵.
对无向图，若边 e_j 是圈 i 的组成部分则 c_ij 为 1 否则为零. 对有向图，若边 e_j 是圈 i 的组成部分则 c_ij 为 1，若边 e_j 在反方向上是圈 i 的组成部分则 c_ij 为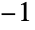，其它情况下则为零.
FindFundamentalCycles 是一个相关的函数，它可被用于返回图的基本循环的列表.

范例

打开所有单元关闭所有单元

基本范例 (2)

找出图的边圈矩阵：

得到图的圈基：

展示这些圈：

范围 (6)

EdgeCycleMatrix 适用于无向图：

有向图：

多重图：

混合图：

用规则指定图：

EdgeCycleMatrix 适用于很大的图：

应用 (1)

得到图的圈基：

创建所有的简单圈：

属性和关系 (3)

用 EdgeList 求得圈的表示：

有 n 个顶点和 m 条边的连通图：

它有大小为 (m-n+1)×m 的边圈矩阵：

从 IncidenceMatrix 计算 EdgeCycleMatrix：

与 EdgeCycleMatrix 比较：

顶部