EstimatedVariogramModel

EstimatedVariogramModel[{loc1val1,loc2val2,…}]

場所 lociで与えられた値 valiから最適なバリオグラム関数を推定する．

EstimatedVariogramModel[{loc1,loc2,…}{val1,val2,…}]

同じ結果を生成する．

EstimatedVariogramModel[…,"model"]

"model"で指定されたバリオグラム関数の最適パラメータを推定する．

EstimatedVariogramModel[…,{"model",params}]

params の非数値パラメータを推定する．

詳細とオプション

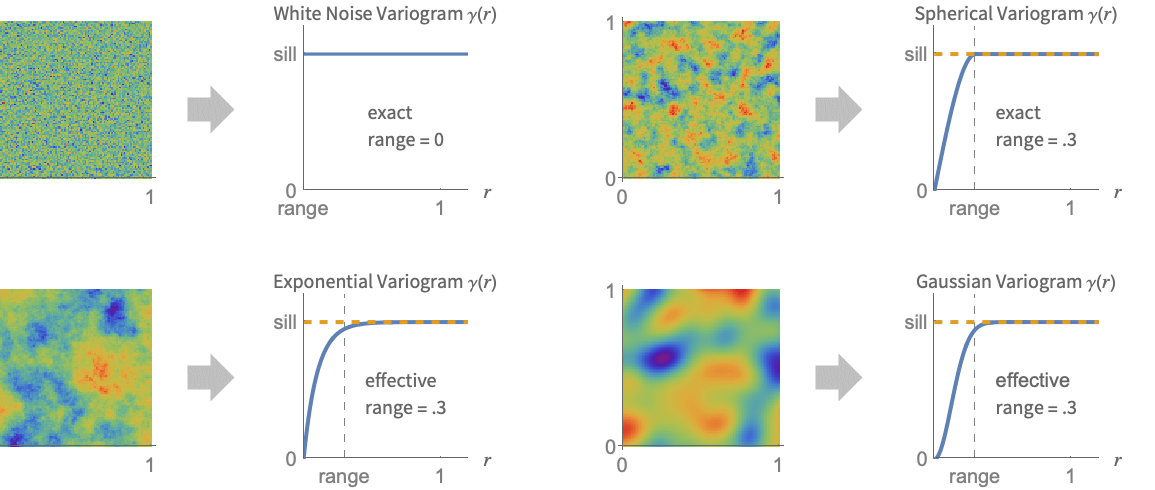
  • バリオグラムモデルは，バリオグラムおよびセミバリオグラムとしても知られている．
  • EstimatedVariogramModelはモデルを空間場データにフィットしてVariogramModelを返す．
  • VariogramModelは，通常，SpatialEstimateにおけるように空間場の値を予測する際に，空間依存の局所モデルとして使われる．
  • 場所 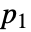と 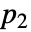における空間過程 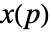のためのバリオグラム 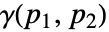は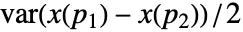で与えられる．これは，過程が空間的にどのくらいの速さで変化するかを測るものである．
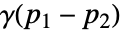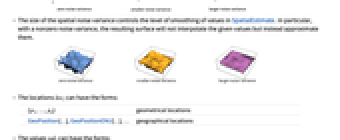
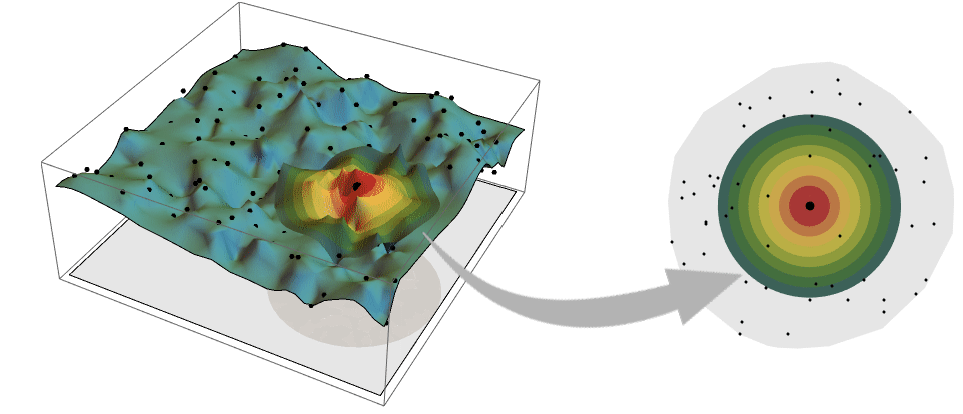
  • 過程が弱定常なら，バリオグラムは場所の差，つまり のみに依存する．過程が等方性の場合は，場所の間の距離，つまり gamma(TemplateBox[{{{p, _, 1}, -, {p, _, 2}}}, Norm])のみに依存する．
  • 次は，対応するバリオグラムと共に定常で等方性がある空間場データの典型的な例である．
  • 自動設定のときは，上記が必要なものすべてであるが，バリオグラムモデルの詳細を制御したいなら，さらに理解すべきことがある．主な2点は平滑化の範囲とレベルである．
  • バリオグラムの範囲は，近くの点に対する依存がどこまで及ぶかを示す．範囲が広いバリオグラムはゆっくり変化する場に対応する．
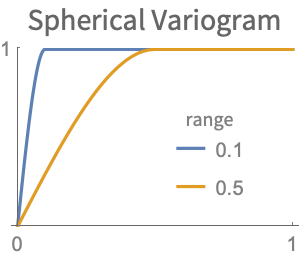
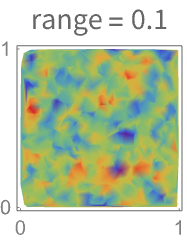
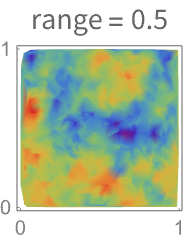
  • バリオグラムの範囲は，点がSpatialEstimateの値の予測範囲に影響するの距離を制御する．
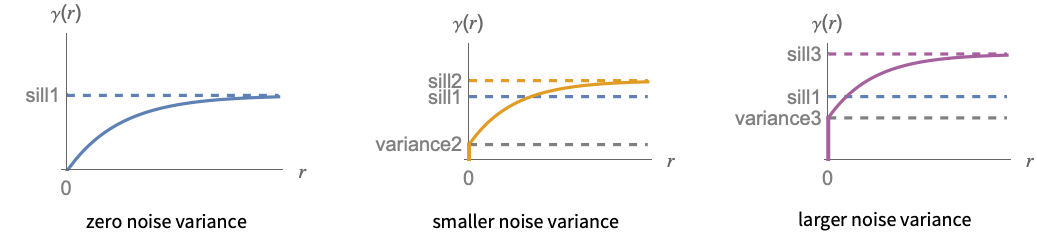
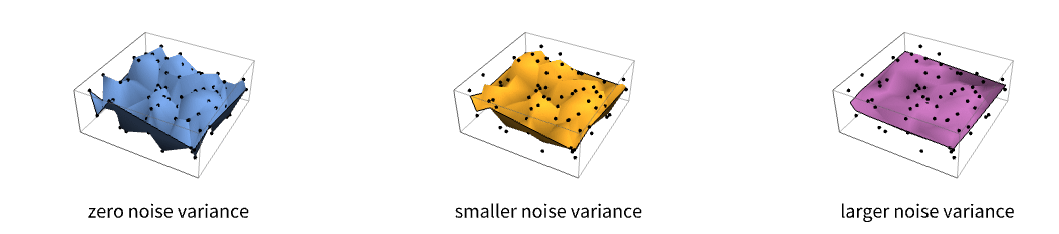
  • 予測の平滑さは，いわゆるバリオグラムの空間ノイズ分散の影響を受ける．これは，原点における値のことである．ホワイトノイズモデル，つまり測定誤差あるいは金塊等のデータの真の不連続性を加えることに相当する．
  • 空間ノイズ分散のサイズはSpatialEstimateにおける値の平滑化レベルを制御する．ノイズ分散が0のときは，結果の曲面は与えられた値を補間せず，代りにそれを近似する．
  • 場所 lociは以下の形式でよい．
  • {p1,…,pd}幾何学的位置
    GeoPosition[…],GeoPositionENU[…],…地理的位置
  • 値 valiは以下の形式でよい．
  • ciスカラー値
    Quantity[ci,"unit"]スカラーの数量
  • 有効な空間バリオグラムになるためには，モデルが整合性の条件を満足しなければならない．有効な空間バリオグラムは非負の関数でなければならず，すべての重み wiについて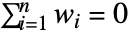，と場所 piのように条件付きで負の明確な条件sum_(i=1)^nsum_(j=1)^nw_i w_j gamma(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm])<=0を満足しなければならない．有効なモデルの族は同種の特徴でグループ化することができる．これらはVariogramModelに列挙されている．
  • 次は，使用可能なオプションである．
  • SpatialNoiseLevel Automaticモデルのノイズ分散を指定する
    SpatialTrendFunction Automatic世界的なトレンドのモデルを指定する

例題

すべて開くすべて閉じる

例  (2)

土壌中の亜鉛濃度のバリオグラムモデルを推定する：

指数バリオグラムモデルを推定する：

シルと範囲の情報を抽出する：

指定の距離における値：

バリオグラム関数をプロットする：

ランダムなデータについてホワイトノイズバリオグラムモデルを推定する：

ホワイトノイズバリオグラムモデルを推定する：

スコープ  (2)

地理データのバリオグラムモデルを推定する：

初期変動が遅いいくつかのモデルをフィットする：

バリオグラムモデルのデータのビニングされたバリオグラムへのフィットを可視化する：

ビニングされたバリオグラムからバリオグラムモデルを推定する：

ビニングされたバリオグラムを計算する：

バリオグラムモデルを推定する：

オプション  (3)

SpatialNoiseLevel  (1)

SpatialNoiseLevelを使ってノイズレベルを指定する：

ゼロノイズレベルを仮定してバリオグラムモデルを推定する：

正のノイズレベルを仮定してバリオグラムモデルを推定する：

モデルのパラメータを比較する：

SpatialTrendFunction  (2)

SpatialTrendFunctionを使ってトレンド関数を指定する：

一定のトレンドを仮定してバリオグラムモデルを推定する：

線形トレンドを仮定してバリオグラムモデルを推定する：

モデルのパラメータを比較する：

線形トレンドがあるデータを見る：

トレンド除去なしで，バリオグラムは無制限のモデルにうまくフィットする：

大規模なトレンドを除去するとミクロスケールの変動がよく分かるようになる：

アプリケーション  (2)

SpatialPointDataについてのバリオグラムモデルを推定する：

BinnedVariogramListを計算してどのモデル族を選ぶべきかのヒントを得る：

いくつかの漸近的バリオグラムモデルをフィットする：

バリオグラムモデルのデータのビニングされたバリオグラムへのフィットを可視化する：

4つのモデルのうち，Maternが最もよくフィットしていて空間推定に使える：

フィット残渣を用いて最適バリオグラムモデルを選択する：

いくつかのバリオグラムモデルをフィットする：

フィットから残渣の重み付きの和を計算する：

データのビニングバリオグラムへのバリオグラムモデルのフィットを可視化する：

残渣の重み付きの和が最小のモデルを選択し，これを使って空間推定を計算する：

考えられる問題  (1)

バリオグラムモデルの中には指定されたデータに相応しくないものがある：

別のモデルに変更する：

Wolfram Research (2021), EstimatedVariogramModel, Wolfram言語関数， https://reference.wolfram.com/language/ref/EstimatedVariogramModel.html.

テキスト

Wolfram Research (2021), EstimatedVariogramModel, Wolfram言語関数， https://reference.wolfram.com/language/ref/EstimatedVariogramModel.html.

CMS

Wolfram Language. 2021. "EstimatedVariogramModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/EstimatedVariogramModel.html.

APA

Wolfram Language. (2021). EstimatedVariogramModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EstimatedVariogramModel.html

BibTeX

@misc{reference.wolfram_2024_estimatedvariogrammodel, author="Wolfram Research", title="{EstimatedVariogramModel}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/EstimatedVariogramModel.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_estimatedvariogrammodel, organization={Wolfram Research}, title={EstimatedVariogramModel}, year={2021}, url={https://reference.wolfram.com/language/ref/EstimatedVariogramModel.html}, note=[Accessed: 18-November-2024 ]}