EventData

EventData[{e1,e2,…}]

明示的に指定された打切り ei持つ事象データを表す．

EventData[{e1,e2,…},{ci1,ci2,…}]

打切り指標 ciiの事象データ eiを表す．

EventData[{e1,e2,…},{cc1,cc2,…}]

打切り数 cciの事象データ eiを表す．

EventData[{e1,e2,…},cspec,{tr1,tr2,…}]

打切りと切断 triの事象データを表す．

詳細

  • EventDataは打切りと切断の情報があるデータを増強する．
  • eiについて次の事象指定を使うことができる．
  • ti打切りなし．事象は tti に発生する
    {ti,∞}右側打切り．事象は ti≤t であるなんらかの t で発生する
    {-∞,ti}左側打切り．事象は t<tiであるなんらかの t で発生する
    {ti,min,ti,max}区間打切り．事象は ti,min<t≤ti,maxであるなんらかの t で発生する
  • ciiには次の打切り指標が使える．
  • 0, None{t,t}打切りなし
    1, Right{t,∞}右側打切り
    -1,Left{-∞,t}左側打切り
  • cciには次の数指定が使える．
  • { ni}eiにおいて ni回の事象
    {ni,ri}eiにおいて ni回の事象と ri回の右側打切り事象
    {ni,ri,li}eiにおいて ni回の事象，ri回の右側打切り事象，li回の左側打切り事象
  • triには次の事象指定を使うことができる．
  • ti,{ti,∞}左側切断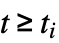．t>=t_(i)で可観測
    {-∞,ti}右側切断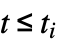．t<=t_(i)で可観測
    {ti,min,ti,max}両側切断．ti,min≤t≤ti,maxで可観測
  • EventDataは以下の統計関数で使うことができる．
  • Mean,Variance,…記述統計関数
    EmpiricalDistribution,…ノンパラメトリック分布推定
    EstimatedDistribution,…パラメトリック分布推定
    SurvivalModelFit,…生存率分析のための関数
  • EventDataの特性はEventData[…]["property"]を指定することで得ることができる．
  • EventData[…]["Properties"]を使って使用可能な特性リストが得られる．
  • EventDataには次の特性がある．
  • "CensoringIndicators"打切り指標{ci1,…}
    "CensoredData"{{t1,∞},…}の形での打切り事象区間
    "EmpiricalPDF"事象の位置と対応する推定された重み
    "InputData"入力事象指定{e1,…}
    "MetaInformation"メタ情報規則のリスト
    "TruncationIntervals"切断区間{tr1,…}
    "CensoringType"存在する最も一般的な打切りのタイプ
    "TruncationType"存在する最も一般的な切断のタイプ

例題

すべて開くすべて閉じる

例  (1)

右側打切りデータの値を示す：

いくつかの記述統計を計算する：

スコープ  (12)

基本的な用法  (5)

事象データの記述統計を計算する：

ノンパラメトリック分布を事象データにフィットする：

パラメトリック分布を事象データにフィットする：

分布と経験的推定をプロットする：

SurvivalModelFitを使ってモデルをフィットする：

信頼帯のある経験的生存関数：

CoxModelFitを使って共変量のあるモデルをフィットする：

パラメトリック推定：

2つのグループの生存率の比較：

打切りと切断の指定  (7)

さまざまな方法で右側打切りを指定する：

オブジェクトはどれも3番目が右側打切りになった同じ4つの観測を表している：

左側打切り：

オブジェクトはどれも3番目が左側打切りになった同じ4つの観測を表している：

区間打切り：

オブジェクトはどれも3番目が区間打切りになった4つの観測を表している：

複数の等価観測を示すために数値を使う：

それぞれのオブジェクトは同じ9つの観測を表している：

左側切断を指定する：

オブジェクトは左側切断で打切りなしのデータを等しく表している：

右側切断を指定する：

オブジェクトは右側切断で打切りなしのデータを表している：

データは打ち切りかつ切断されることができる：

オブジェクトは右側打切りで左側切断のデータを表している：

アプリケーション  (1)

推定生存関数のプロットで右側打切りをマークする：

推定生存関数：

打切りマーカを作る：

推定生存関数のプロットと打切りマーカを示す：

特性と関係  (1)

記述統計は潜在的なSurvivalDistributionに基づいている：

サンプル推定は母集団推定と異なるときに与えられる：

Wolfram Research (2012), EventData, Wolfram言語関数， https://reference.wolfram.com/language/ref/EventData.html.

テキスト

Wolfram Research (2012), EventData, Wolfram言語関数， https://reference.wolfram.com/language/ref/EventData.html.

CMS

Wolfram Language. 2012. "EventData." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/EventData.html.

APA

Wolfram Language. (2012). EventData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EventData.html

BibTeX

@misc{reference.wolfram_2024_eventdata, author="Wolfram Research", title="{EventData}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/EventData.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_eventdata, organization={Wolfram Research}, title={EventData}, year={2012}, url={https://reference.wolfram.com/language/ref/EventData.html}, note=[Accessed: 18-November-2024 ]}