FinancialDerivative

FinancialDerivative[instrument,params,ambientparams]

gives the value of the specified financial instrument.

FinancialDerivative[instrument,params,ambientparams,prop]

computes the specified property prop.

Details and Options

  • FinancialDerivative can compute the values and partial derivatives for many common types of financial derivative contracts.
  • FinancialDerivative[] gives a list of available contracts.
  • Contracts are typically specified as a list of the form {option,exercise,type}, where option is the name of the financial instrument, exercise is normally "European" or "American", and type is either "Call" or "Put".
  • FinancialDerivative["CUDA"] gives a list of contracts that are CUDA accelerated. This feature is available only in Wolfram Finance Platform. »
  • The option "RuntimeTarget" specifies the target devices such as CPUs and GPUs where the derivative computation takes place. This feature is available only in Wolfram Finance Platform. »
  • The settings for "RuntimeTarget" include Automatic, "CUDA" and "Generic". »
  • FinancialDerivative[instrument] lists the names of the contract and ambient parameters.
  • FinancialDerivative[instrument,params,ambientparams] computes the value of instrument for the specified ambient parameters.
  • FinancialDerivative[instrument,params,ambientparams,{prop1,prop2,…}] computes multiple properties.
  • FinancialDerivative[instruments,params,ambientparams,"Rules"] computes all available properties and returns the result as a list of rules.
  • Typical contract parameters include:
  • "StrikePrice"strike price
    "Expiration"expiration date, or time until expiration
  • The expiration date can be specified as a date or as the time left to maturity.
  • Ambient parameters common to all option types:
  • "CurrentPrice"price of the underlying asset at the reference time
    "Volatility"current volatility of the underlying asset
    "InterestRate"risk-free interest rate
    "Dividend"dividend paid per time unit
    "ReferenceTime"reference date or time
  • For options on multiple underlying assets, ambient parameters can be given as a list or as a single value common to all underlying assets.
  • Volatilities, interest rates, dividends, and the maturity time are assumed to refer to the same time unit, typically years.
  • The reference time can be given as a date or as a time difference. If it is not specified, the value is assumed to be today's date.
  • Ambient parameter required for basket options, which involve multiple underlying assets:
  • "CorrelationMatrix"correlation matrix for underlying assets
  • The correlation between underlying assets is given as a real symmetric matrix with 1s on the diagonal. All correlation coefficients are in the range 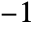to .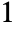
  • The correlation matrix can also be given as a flat list of the coefficients above the diagonal.
  • Ambient currency parameters relevant to Quanto options:
  • "ExchangeRate"current price of the foreign currency
    "ExchangeVolatility"volatility of the foreign exchange
    "ForeignInterestRate"risk-free interest rate in the foreign currency
  • Properties computed by FinancialDerivative include:
  • "Value"value on the reference date
    "CriticalValue"critical value for American options
    "Delta"derivative of the value with respect to the price
    "Gamma"second derivative of the value with respect to the price
    "Rho"derivative of the value with respect to the interest rate
    "Theta"derivative of the value with respect to the time until expiration
    "Vega"derivative of the value with respect to the volatility
    "Greeks"all Greeks, given as a list of rules {delta,gamma,rho,theta,vega}
    "ImpliedVolatility"volatility implied by the contract price
  • FinancialDerivative takes the following options:
  • "GridSize" Automaticgrid size for finite-difference methods, in the form {xgrid,tgrid}
    "Paths" Automaticnumber of paths used in a simulation-based solver
    "Steps" Automaticnumber of steps in each path
    Method Automatica specific solution method, when available
    "Caching" Falsevalue caching, when available
  • Asian Options
  • Asian options have a payoff that is the difference between the strike price and the average value of the underlying asset over the lifetime of the contract. FinancialDerivative can price the following types of Asian options:
  • "AsianArithmetic"arithmetic mean Asian option
    "AsianGeometric"geometric mean Asian option
  • Contract parameters:
  • "Inception"inception date of the contract, or lifetime so far
    "Expiration"expiration date, or time to maturity
    "AverageSoFar"average price since inception
    "StrikePrice"strike price
  • FinancialDerivative supports Asian call and put options with European exercise style.
  • Barrier Options
  • Barrier options have a payoff that depends on whether or not the price reaches a predetermined barrier level. The following types of barrier options are supported:
  • "BarrierDownIn"barrier down-and-in option
    "BarrierDownOut"barrier down-and-out option
    "BarrierUpIn"barrier up-and-in option
    "BarrierUpOut"barrier up-and-out option
  • Barrier up-and-out options become void if the price rises to or exceeds the barrier level. Down-and-out options become void if the price decreases to the barrier. Up-and-in options become valid as the price rises to the barrier level. Down-and-in options become valid when the price falls to or below the barrier level.
  • All single-barrier options require the following parameters:
  • "Barrier"barrier level
    "Expiration"expiration date, or time to maturity
    "Rebate"rebate paid to option holder if the option expires void
    "StrikePrice"strike price
  • FinancialDerivative supports call and put barrier options with European and American exercise styles. All rebates are paid at option expiration.
  • Binary Options
  • Binary or digital options have a payoff at maturity that is either a fixed amount or nothing.
  • "BinaryCash"binary cash-or-nothing option
    "BinaryAsset"binary asset-or-nothing option
  • Binary cash-or-nothing options pay a fixed amount if the underlying price is in the money at maturity. Binary asset-or-nothing options pay the current price of the asset at expiration if the price of the asset is above the strike price.
  • Binary options require the following parameters:
  • "Expiration"expiration date, or time to maturity
    "StrikePrice"strike price
  • FinancialDerivative supports binary call and put options with European exercise style. The payoff is taken to be 1 for the binary cash option.
  • Chooser Options
  • A chooser option is a compound contract that requires the buyer to choose between a call and a put option on the same underlying asset at a predetermined expiration time.
  • "Chooser"chooser option
  • Required contract parameters:
  • "Expiration"choice date, or time until choice
    "ExpirationCall"expiration date of the underlying call option
    "ExpirationPut"expiration date of the underlying put option
    "StrikePriceCall"strike price of the call option
    "StrikePricePut"strike price of the put option
  • FinancialDerivative supports chooser options with European exercise style.
  • Compound Options
  • A compound contract is an option on a European vanilla option.
  • "CompoundCall"underlying asset is a call option
    "CompoundPut"underlying asset is a put option
  • Required contract parameters:
  • "Expiration"expiration date of the compound option
    "ExpirationUnderlying"expiration date of the underlying option
    "StrikePrice"strike price of the compound option
    "StrikePriceUnderlying"strike price of the underlying option
  • f supports compound call and put options with European exercise style.
  • Double-Barrier Options
  • Double-barrier options have a payoff that depends on whether or not the price of the underlying asset reaches either of the two barrier levels at any time prior to exercise. The following types of double-barrier options are supported:
  • "DoubleBarrierKnockOut"double barrier knock-out option
    "DoubleBarrierKnockIn"double barrier knock-in option
  • A double-barrier knock-out option becomes void as soon as the price of the underlying asset breaks out of the barrier interval. A double-barrier knock-in option becomes valid as soon as the price breaks out of the interval.
  • Required contract parameters:
  • "Expiration"expiration date, or time to maturity
    "StrikePrice"contract strike price
    "Barriers"barrier interval in the form {lower,upper}
  • FinancialDerivative supports double-barrier call and put options with either American or European exercise style.
  • Extendible Options
  • Extendible options can be exercised at the time of maturity, or they can be extended by a predetermined period. The following types of extendible options are supported:
  • "ExtendibleHolder"holder-extendible option
    "ExtendibleWriter"writer-extendible option
  • A holder-extendible option requires the holder to pay an additional premium to extend the option. A writer-extendible option is extended automatically if the option is out of the money upon initial expiration.
  • Required contract parameters:
  • "Expiration"expiration date, or time to maturity
    "StrikePrice"contract strike price
    "StrikePriceAdjusted"contract strike price after extension
    "ExtensionPeriod"extension period, or time to which extended
    "ExtensionFee"additional premium to be paid for extension ("ExtendibleHolder" only)
  • FinancialDerivative supports extendible call and put options with European exercise style.
  • Lookback Options
  • A lookback contract is a path-dependent option whose value at exercise depends on the optimal price of the underlying asset over the lifetime of the contract. The following lookback options are supported:
  • "LookbackFloating"floating-strike lookback option
    "LookbackFixed"fixed-strike lookback option
  • In a floating-strike lookback call option, the strike price is taken to be the lowest price attained by the underlying asset over the option's lifetime. For put options, the highest underlying price is used.
  • In a fixed-strike lookback call option, the value of the underlying asset at exercise is taken to be the highest price of the underlying asset over the option's lifetime. For put options, the lowest underlying price is used.
  • Required contract parameters:
  • "Expiration"expiration date, or time to maturity
    "StrikePrice"contract strike price ("LookbackFixed" only)
    "MaxSoFar"highest value attained by the asset over the contract period to date ("LookbackFixed" call option or "LookbackFloating" put option)
    "MinSoFar"lowest value attained by the asset over the contract period to date ("LookbackFixed" put option or "LookbackFloating" call option)
  • FinancialDerivative supports lookback call and put options with European exercise style. In addition, it supports American exercise for floating-strike lookback options.
  • One-Touch Options
  • A one-touch contract is a binary option with an American exercise style.
  • "OneTouch"one touch option
  • One-touch options pay a fixed amount at an arbitrary exercise time if the option is in the money.
  • Required contract parameters:
  • "Expiration"expiration date, or time to maturity
    "StrikePrice"contract strike price
  • FinancialDerivative supports one-touch call and put options. The payoff is taken to be 1.
  • Option on Future
  • An option on a future has a forward contract, rather than a stock security, as its underlying asset.
  • "Future"option on a future
  • Required contract parameters:
  • "Expiration"expiration date, or time to maturity
    "StrikePrice"contract strike price
  • FinancialDerivative supports European call and put options on futures.
  • Perpetual Vanilla Options
  • A perpetual vanilla contract is an American vanilla option without an expiration date.
  • "Perpetual"perpetual vanilla option
  • Required contract parameters:
  • "StrikePrice"contract strike price
  • FinancialDerivative supports American call and put perpetuals.
  • Perpetual Lookback Options
  • A perpetual lookback contract is a lookback contract without an expiration date.
  • "PerpetualLookback"floating-strike perpetual lookback option
  • In a floating-strike perpetual lookback call option, the strike price adjusts to the lowest price attained by the asset over the contract period so far. For put options, the strike price is taken to be the highest underlying price so far.
  • Required contract parameters:
  • "MaxSoFar"highest asset value over the contract period so far (put)
    "MinSoFar"lowest asset value over the contract period so far (call)
  • FinancialDerivative supports floating-strike perpetual lookback call and put options.
  • Power Options
  • A power option is a contract for which the payoff is raised to a power.
  • "Power"power option
    "Powered"powered option
    "PowerCapped"capped power option
  • A power option raises the price of the underlying asset at time of exercise to the power specified. A powered option raises the difference between the price of the underlying asset and the strike price to the power specified. A capped power option caps the payoff on a power option.
  • Required contract parameters:
  • "Expiration"expiration date, or time to maturity
    "StrikePrice"contract strike price
    "Power"the power
    "Cap"the maximum payoff (capped power option)
  • Russian Options
  • A Russian option is a type of perpetual lookback call option for which the payoff is the highest value attained by the underlying asset by exercise time.
  • "Russian"fixed-strike perpetual lookback option
  • Required contract parameters:
  • "MaxSoFar"highest asset value over the contract period to date
  • Vanilla Options
  • A vanilla option contract is a path-independent option.
  • "Vanilla"vanilla option
  • Required contract parameters:
  • "Expiration"expiration date, or time to maturity
    "StrikePrice"contract strike price
  • FinancialDerivative supports vanilla call and put options with either an American or a European exercise style. The "Vanilla" name specification can be omitted.
  • By default, FinancialDerivative prices American vanilla options by numerically solving the Black–Scholes partial differential equation. A binomial tree solution method can be specified by setting the Method option to "Binomial".
  • Rainbow Options
  • A rainbow contract entitles the option holder to the maximum of the payouts generated by the individual components of a basket of assets.
  • Option names:
  • "RainbowBest"payout is the value of the best-performing asset
    "RainbowWorst"payout is the value of the worst-performing asset
    "RainbowMoney"payout is based on the value of the best-performing asset, where a risk-free investment is one of the assets
  • Required contract parameters:
  • "Expiration"expiration date, or time to maturity
    "Money"amount of cash in the basket ("RainbowMoney" option)
  • FinancialDerivative supports rainbow options with American and European exercise styles. American exercise is supported for a maximum of two non-cash assets in a basket.
  • Rainbow Minimum and Maximum Options
  • A rainbow minimum contract has a payout that is the value of an option on the worst-performing asset for a call, and on the best-performing asset for a put. A rainbow maximum contract has a payout that is the value of an option on the best-performing asset for a call, and on the worst-performing asset for a put.
  • Option names:
  • "RainbowMin"rainbow minimum contract
    "RainbowMax"rainbow maximum contract
  • Required contract parameters:
  • "Expiration"expiration date, or time to maturity
    "StrikePrice"contract strike price
  • FinancialDerivative supports rainbow minimum and maximum call and put options with American and European exercise styles. American exercise is supported for a maximum of two assets in a basket.
  • Mountain Range Options
  • Mountain range options are a class of contracts that entitle the holder to a payout that is based on the performance of a basket of assets, with certain time constraints on asset performance.
  • "Altiplano"Altiplano mountain range contract
    "Annapurna"Annapurna mountain range contract
    "Atlas"Atlas mountain range contract
    "Everest"Everest mountain range contract
    "Himalaya"Himalaya mountain range contract
  • Exercise and option type specifications are not applicable to mountain range options.
  • An Altiplano contract is a type of mountain range option that pays out a fixed coupon amount if none of the basket assets have reached their respective barriers, and nothing otherwise.
  • Parameters for Altiplano contracts:
  • "Barriers"barrier values of each asset
    "Coupon"coupon amount
    "Expiration"expiration date, or time to maturity
  • An Annapurna contract pays out a fixed coupon amount if none of the basket assets descend below their respective fractional barrier prices, and nothing otherwise.
  • Parameters for Annapurna options:
  • "Fractions"asset price fractions that trigger the validity condition
    "Coupon"coupon amount
    "Expiration"expiration date, or time to maturity
  • An Atlas contract has a payout that is based on the performance of a basket from which the best- and worst-performing assets have been removed.
  • Parameters for Atlas contracts:
  • "StrikePrice"strike price of the option, expressed as a multiplicative factor
    "NominalAmount"cash amount on which the returns of the option accrue
    "Expiration"expiration date, or time to maturity
  • An Everest contract has a payout that is based on the performance of the worst asset in a basket of assets.
  • Parameters for Everest contracts:
  • "NominalAmount"cash amount on which the returns of the option accrue
    "Expiration"expiration date, or time to maturity
  • A Himalaya contract has a payout that is based on the performance of the best asset in a gradually shrinking basket of assets. The time to expiration is divided into subperiods, with the yield for each subperiod determined by the return on the best-performing asset over that period, and with each asset being used to determine a subperiod return exactly once.
  • Parameters for Himalaya contracts:
  • "NominalAmount"cash amount on which the returns of the option accrue
    "Expiration"expiration date, or time to maturity
  • Spread Options
  • A spread contract is a multi-asset option whose value depends on the difference between the values of the underlying assets at the time of exercise.
  • "Spread"two-asset spread option
  • Required contract parameters:
  • "Expiration"expiration date, or time to maturity
    "StrikePrice"contract strike price
  • FinancialDerivative supports spread call and put options with American and European exercise styles.
  • Quanto Vanilla Options
  • A Quanto vanilla contract is an option whose value at exercise depends on the performance of the underlying asset, as well as on the performance of the currency in which the asset is denominated.
  • Option names:
  • "QuantoFixedExchange"vanilla fixed-exchange Quanto option
    "QuantoFixedStrike"vanilla fixed-strike Quanto option
  • A vanilla fixed-exchange Quanto option is settled at a predetermined exchange rate. A vanilla fixed-strike Quanto option is settled at a fixed strike price in a foreign currency at the prevailing exchange rate.
  • Required contract parameters:
  • "Expiration"expiration date, or time to maturity
    "StrikePrice"contract strike price
  • FinancialDerivative supports vanilla Quanto call and put options with American and European exercise styles.

Examples

open allclose all

Basic Examples  (6)

Value of a European call option:

Value and all Greeks of a European call option:

Compute the value given an expiration date of the contract:

List all available contract types:

List all contracts that are CUDA accelerated:

Maximize the performance of the derivative valuation using GPUs and parallelizing computation by giving parameters in lists:

Scope  (30)

Contract Types  (27)

Vanilla  (3)

Determine the parameters for a vanilla contract:

Value of a American vanilla contract:

Compute the difference in values of an American and a European vanilla contract:

Compute the implied volatility of the contract:

Asian  (3)

Compute the value of an Asian option:

The value of the option is correlated with the weight of the average:

Compute the value and Greeks of an Asian arithmetic call option:

Barrier  (2)

Compute the value of a barrier option:

Barriers restrict positive outcomes for the option holder, compared to a vanilla contract:

Compute the value of a double-barrier knock-out option:

Compound  (3)

Compute the value of a European exercise call on a call option:

An extendible contract for the same parameters is at least as valuable as a compound option:

A chooser option for the same parameters will be more expensive than either:

Lookback  (3)

Compute the deltas of a lookback fixed-strike and a lookback floating-strike option:

Compute the volatility needed to produce a given critical value for a perpetual lookback put:

Plot the effect of volatility on the critical values of perpetuals:

Power  (3)

Compute the value of a standard European power call option:

Compute the value of a European powered put option:

Compute the value of a European capped power put option:

Rainbow  (5)

Compute the value of a rainbow best option:

Compute the value and Greeks of a rainbow max call option:

Specify the correlation matrix in the upper-triangular form, and dividends and volatilities as common values:

A rainbow money option is a hedge against poor performance by all basket components:

Plot basket performance ranges as a function of volatility:

Range  (5)

Compute the value of a Himalaya contract:

Compute vega, theta, and rho of an Annapurna contract:

Range contract values are computed using a simulation, and are subject to a small uncertainty:

Atlas option with a return strike price of 1 computes the normalized average yield of a basket of stocks accruing on the nominal amount specified:

The returns accrue on the nominal amount, so the current asset prices are not important:

Dates  (3)

All date specifications must be consistent:

All rates are assumed to be denominated in the same time unit, usually years:

Obtain the same value by specifying daily rates instead:

Options  (12)

Method  (1)

Compute the value of an option by a nondefault method:

"GridSize"  (2)

A short time to expiration requires fewer grid points in the time domain:

Raise the sensitivity to the ambient parameters by constructing a finer spatial grid:

"Paths"  (2)

Change the default number of paths for a simulation-based solver:

Quadrupling the number of samples halves the error:

"RuntimeTarget"(option available in Wolfram Finance Platform only)  (3)

By default, the option setting "RuntimeTarget"->Automatic chooses the fastest available runtime target:

The option setting "RuntimeTarget"->"CUDA" forces the runtime target to be GPUs with CUDA capability:

The settings "Device" and "TargetPrecision" can be used to specify a target CUDA device and desired precision, respectively:

In general, the setting "TargetPrecision"->"Double" can yield more precise results than the "TargetPrecision"->"Single" setting.

The option setting "RuntimeTarget"->"Generic" forces the runtime target to be a local CPU:

"Steps"  (3)

For range options with barriers, the step parameter determines the frequency with which each path is sampled:

For Asian options, the step parameter represents the number of times the average is taken along each price path:

Control the number of steps in a binomial tree algorithm:

"Caching"  (1)

For basket and Asian options, Caching->True enables the caching of values related to the Monte Carlo solution method. By default, Caching->False:

Applications  (3)

Plot the return surface of a call spread:

Plot the values of Greeks as a function of time left until expiration:

Plot the critical value surface of an American put contract:

Properties & Relations  (1)

Confirm that delta is the contract sensitivity to the current price by plotting its Legendre transform:

Possible Issues  (1)

Default spatial grid size does not ensure accuracy for some parameter choices:

Wolfram Research (2010), FinancialDerivative, Wolfram Language function, https://reference.wolfram.com/language/ref/FinancialDerivative.html (updated 2012).

Text

Wolfram Research (2010), FinancialDerivative, Wolfram Language function, https://reference.wolfram.com/language/ref/FinancialDerivative.html (updated 2012).

CMS

Wolfram Language. 2010. "FinancialDerivative." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/FinancialDerivative.html.

APA

Wolfram Language. (2010). FinancialDerivative. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FinancialDerivative.html

BibTeX

@misc{reference.wolfram_2024_financialderivative, author="Wolfram Research", title="{FinancialDerivative}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/FinancialDerivative.html}", note=[Accessed: 26-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_financialderivative, organization={Wolfram Research}, title={FinancialDerivative}, year={2012}, url={https://reference.wolfram.com/language/ref/FinancialDerivative.html}, note=[Accessed: 26-December-2024 ]}