FinancialDerivative

FinancialDerivative[instrument,params,ambientparams]

给出指定金融工具的价值.

FinancialDerivative[instrument,params,ambientparams,prop]

计算指定的属性 prop.

更多信息和选项

  • FinancialDerivative 能够计算多种常见类型的金融衍生产品合约的价值和偏导.
  • FinancialDerivative[] 给出一个可用合约的列表.
  • 合约通常以形如 {option,exercise,type} 的列表形式指定，其中 option 是金融工具的名称，exercise 通常是 "European" 或 "American"，type 为 "Call" 或 "Put".
  • FinancialDerivative["CUDA"] 给出一个由 CUDA 加速的合约列表. 该功能仅可在 Wolfram 金融平台（Wolfram Finance Platform）中使用. »
  • 选项 "RuntimeTarget" 指定了进行衍生品计算的目标设备. 该功能仅可在 Wolfram 金融平台（Wolfram Finance Platform）中使用. »
  • "RuntimeTarget" 的设置包括 Automatic、"CUDA" 和 "Generic". »
  • FinancialDerivative[instrument] 列出合约名称和环境参数.
  • FinancialDerivative[instrument,params,ambientparams] 计算指定环境参数下 instrument 的值.
  • FinancialDerivative[instrument,params,ambientparams,{prop1,prop2,…}] 计算多个属性.
  • FinancialDerivative[instruments,params,ambientparams,"Rules"] 计算所有可用属性并以规则列表的形式返回结果.
  • 典型合约参数包括：
  • "StrikePrice"执行价格
    "Expiration"到期日，或距到期日的时间
  • 到期日可以指定为日期，或者距离到期日的时间.
  • 通用于所有选项类型的环境参数：
  • "CurrentPrice"标的资产在基准时刻的价格
    "Volatility"标的资产的当前波动率
    "InterestRate"无风险利率
    "Dividend"单位时间所支付的股息
    "ReferenceTime"基准日期或基准时间
  • 对于多个标的资产的期权，环境参数可以以列表形式给出，或用一个通用于所有标的资产的单值给出.
  • 波动率、利率、股息及到期时间假定使用相同的时间单位，通常以年为单位.
  • 基准时间可以采用日期的形式或者是一个时间差. 如果不指定，则取值为今天的日期.
  • 组合型期权所要求的环境参数，涉及到多个标的资产：
  • "CorrelationMatrix"标的资产的相关矩阵
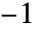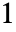  • 标的资产之间的相关性以实对称矩阵形式给出，对角线元素为1. 所有相关系数在 到 之间.
  • 相关矩阵也可以以对角线上方系数的展平列表形式给出.
  • 与汇率连动期权相关的环境货币参数：
  • "ExchangeRate"外币的当前价格
    "ExchangeVolatility"外汇波动率
    "ForeignInterestRate"外币的无风险利率
  • 由 FinancialDerivative 计算的属性包括：
  • "Value"基准日期的价值
    "CriticalValue"美式期权的临界值
    "Delta"价值关于价格的导数
    "Gamma"价值关于价格的二阶导数
    "Rho"价值关于利率的导数
    "Theta"价值关于到期时间的导数
    "Vega"价值关于波动率的导数
    "Greeks"所有的Greek，以规则列表形式给出{delta,gamma,rho,theta,vega}
    "ImpliedVolatility"由合约价格决定的隐含波动率
  • FinancialDerivative 取下列选项：
  • "GridSize" Automatic有限差分法的网格尺寸，形式为 {xgrid,tgrid}
    "Paths" Automatic用于基于仿真求解程序的路径数
    "Steps" Automatic各路径的步长数目
    Method Automatic当可用时，一个具体的解决方法
    "Caching" False价值缓存，当可用时
  • 亚式期权
  • 亚式期权是这样一类期权，其到期日价值为执行价格与标的资产在合约有效期内的平均价格之差. FinancialDerivative 可对下列类型的亚式期权定价：
  • "AsianArithmetic"算术平均亚式期权
    "AsianGeometric"几何平均亚式期权
  • 合约参数：
  • "Inception"合约起保日，或当前算起的有效期
    "Expiration"到期日，或到期期限
    "AverageSoFar"从起保日算起的平均价格
    "StrikePrice"执行价格
  • FinancialDerivative 支持欧式执行风格的亚式看涨、看跌期权.
  • 障碍期权
  • 障碍期权的收益取决于标的资产的价格是否触及一个预先确定的界限. 支持下列类型的障碍期权：
  • "BarrierDownIn"下降入局障碍期权
    "BarrierDownOut"下降出局障碍期权
    "BarrierUpIn"上升入局障碍期权
    "BarrierUpOut"上升出局障碍期权
  • 上升出局障碍期权在价格涨至或超过障碍水平时失效. 下降出局期权在价格降至障碍水平时失效. 上升入局期权在价格升至障碍水平时有效. 下降入局期权在价格降至或低于障碍水平时有效.
  • 所有单一障碍期权要求有下列参数：
  • "Barrier"障碍水平
    "Expiration"到期日，或到期期限
    "Rebate"如果期权无效作废时支付给期权持有人的回扣（rebate）
    "StrikePrice"执行价格
  • f 支持欧式行使方式的复合看涨和看跌期权.
  • 二元期权
  • 二元期权或称数字期权在到期日的收益只有两种可能：一个固定金额，或零.
  • "BinaryCash"现金型二元期权（现金或无价值）
    "BinaryAsset"资产型二元期权（资产或无价值）
  • 现金型二元期权当标的资产价格在到期日处于价内时，支付一固定金额. 资产型二元期权当标的资产价格高于执行价格时支付到期日资产的价格.
  • 二元期权要求有下列参数：
  • "Expiration"到期日，或到期期限
    "StrikePrice"执行价格
  • FinancialDerivative 支持欧式执行风格的二元看涨、看跌期权. 现金型二元期权的收益取为1.
  • 选择期权
  • 选择期权是一种复合合约，要求买方选择在预先确定的到期日从同一标的资产的看涨和看跌期权中选择其一.
  • "Chooser"选择期权
  • 需要的合约参数：
  • "Expiration"选择日期，或距选择的时间
    "ExpirationCall"标的看涨期权的到期日
    "ExpirationPut"标的看跌期权的到期日
    "StrikePriceCall"看涨期权的执行价格
    "StrikePricePut"看跌期权的执行价格
  • FinancialDerivative 支持欧式执行风格的选择期权.
  • 复合期权
  • 复合合约是一种基于欧式标准期权的期权.
  • "CompoundCall"标的资产为看涨期权
    "CompoundPut"标的资产为看跌期权
  • 需要的合约参数：
  • "Expiration"复合期权的到期日
    "ExpirationUnderlying"标的期权的到期日
    "StrikePrice"复合期权的执行价格
    "StrikePriceUnderlying"标的期权的执行价格
  • FinancialDerivative 支持欧式执行风格的复合看涨和看跌期权.
  • 双重障碍期权
  • 双重障碍期权的收益取决于标的资产价格在到期日之前是否触及两个障碍水平中的任意一个. 支持下列两种类型的双重障碍期权：
  • "DoubleBarrierKnockOut"双重障碍敲出期权
    "DoubleBarrierKnockIn"双重障碍敲入期权
  • 双重障碍敲出期权一旦标的资产价格突破障碍区间即作废. 双重障碍敲入期权一旦标的资产价格突破障碍区间即有效.
  • 需要的合约参数：
  • "Expiration"到期日，或到期期限
    "StrikePrice"合约执行价格
    "Barriers"形如 {lower,upper}的障碍区间
  • FinancialDerivative 支持美式或欧式执行风格的所有双重障碍看涨、看跌期权.
  • 可延期期权
  • 可延期期权可以在到期日执行，也可以延长一个预先确定的时间. 支持下列两种类型的可延长期权：
  • "ExtendibleHolder"期权持有人可延期期权
    "ExtendibleWriter"期权卖方可延期期权
  • 期权持有人可延期期权要求持有人支付额外的期权费以延长期权. 期权卖方可延期期权当期权在初始到期日处于价外时自动延期.
  • 需要的合约参数：
  • "Expiration"到期日，或到期期限
    "StrikePrice"合约执行价格
    "StrikePriceAdjusted"延期后的合约执行价格
    "ExtensionPeriod"延期时间，或所延长至的时间
    "ExtensionFee"延期所支付的额外期权费（仅对 "ExtendibleHolder"）
  • FinancialDerivative 支持欧式执行风格的可延期看涨和看跌期权.
  • 回顾期权
  • 回顾期权与路径有关，其在执行日的价值取决于标的资产在合约有效期内的最优价格. 支持下列回顾期权：
  • "LookbackFloating"执行价格浮动的回顾期权
    "LookbackFixed"执行价格固定的回顾期权
  • 对于执行价格浮动的回顾式看涨期权，执行价格取标的资产在期权有效期内所触及的最低价格. 对于看跌期权，则取最高标的价格.
  • 对于执行价格固定的回顾式看涨期权，标的资产在到期日的价值取期权有效期内标的资产的最高价格. 对于看跌期权，则取最低标的价格.
  • 需要的合约参数：
  • "Expiration"到期日，或到期期限
    "StrikePrice"合约执行价格（仅适用于 "LookbackFixed"）
    "MaxSoFar"到目前为止，标的资产在合约期内所触及的最高值 ("LookbackFixed" 看涨期权或者 "LookbackFloating" 看跌期权)
    "MinSoFar"到目前为止，标的资产在合约期内所触及的最低值 ("LookbackFixed" 看涨期权或者 "LookbackFloating" 看跌期权)
  • FinancialDerivative 支持欧式执行风格的回顾式看涨与看跌期权. 此外，对于执行价格浮动的回顾式期权，也支持美式执行风格.
  • 一触即付期权
  • 一触即付期权是一种美式执行风格的二元期权.
  • "OneTouch"一触即付期权
  • 如果处于价内，一触即付期权在一任意执行日期支付固定的金额.
  • 需要的合约参数：
  • "Expiration"到期日，或到期期限
    "StrikePrice"合约执行价格
  • FinancialDerivative 支持一触即付式看涨与看跌期权. 收益取值为1.
  • 期货期权
  • 期货期权的标的资产是一种远期合约，而非股票证券.
  • "Future"期货期权
  • 需要的合约参数：
  • "Expiration"到期日，或到期期限
    "StrikePrice"合约执行价格
  • FinancialDerivative 支持欧式看涨与看跌期货期权.
  • 永久标准期权
  • 永久标准期权是一种无到期日的美式标准期权.
  • "Perpetual"永久标准期权
  • 需要的合约参数：
  • "StrikePrice"合约执行价格
  • FinancialDerivative 支持美式看涨与看跌永久标准期权.
  • 永久回顾期权
  • 永久回顾期权是一种无到期日的回顾合约.
  • "PerpetualLookback"执行价格浮动的永久回顾期权
  • 对于执行价格浮动的永久回顾看涨期权，执行价格调整至标的资产自期权有效期开始到目前为止所触及的最低价格. 对于看跌期权，执行价格取值为目前为止标的最高标的价格.
  • 需要的合约参数：
  • "MaxSoFar"到目前为止，标的资产在合约期内的最高值（看跌期权）
    "MinSoFar"到目前为止，标的资产在合约期内的最低值（看涨期权）
  • FinancialDerivative 支持执行价格浮动的永久回顾型看涨与看跌期权.
  • 幂式期权
  • 购买力期权是损益提高到平方的合约
  • "Power"幂式期权
    "Powered"加幂期权
    "PowerCapped"封顶幂式期权
  • 幂式期权将履约时的内在资产价格提高到指定的幂次. 加幂（powered）期权把内在资产和预购价格提高到指定的幂次. 封顶幂式期权限制了幂式期权的最大回报.
  • 需要的合约参数：
  • "Expiration"到期日，或者到期期限
    "StrikePrice"合同履约价
    "Power"购买力
    "Cap"最大回报（封顶购买力期权）
  • 俄式期权
  • 俄式期权是一种永久回顾型看涨期权，其收益为标的资产在到期日之前所触及的最高值.
  • "Russian"执行价格固定的永久回顾期权
  • 需要的合约参数：
  • "MaxSoFar"到目前为止，标的资产在合约期内的最高值
  • 标准期权
  • 标准期权合约是一种与路径无关的期权.
  • "Vanilla"标准期权
  • 需要的合约参数：
  • "Expiration"到期日，或到期期限
    "StrikePrice"合约执行价格
  • FinancialDerivative 支持美式或欧式执行风格的标准看涨与看跌期权. "Vanilla" 的名称指定可以忽略.
  • 默认时，FinancialDerivative 通过数值式求解 Black–Scholes 偏微分方程对美式标准期权定价.二项树解法可以通过设定 "Binomial" 的 Method 选项指定.
  • 彩虹期权
  • 彩虹期权是期权持有者有权得到由一组资产个别组分产生的最大支付.
  • 选项名称：
  • "RainbowBest"支付额为表现最好的资产值
    "RainbowWorst"支付额为表现最差的资产值
    "RainbowMoney"支付额基于表现最好的资产值，其中有一个无风险投资为资产之一
  • 需要的合约参数：
  • "Expiration"到期日，或到期期限
    "Money"资产组合中的现金额（"RainbowMoney" 期权）
  • FinancialDerivative 支持美式与欧式执行风格的彩虹期权. 如果是美式执行风格，只支持一组资产中至多含有两种非现金资产的情况.
  • 彩虹最小与最大式期权
  • 彩虹最小式期权的支付是表现最差资产的看涨期权价值，是表现最好资产的看跌期权价值. 彩虹最大式期权的支付是表现最好资产的看涨期权价值，是表现最差资产的看跌期权价值.
  • 选项名称：
  • "RainbowMin"彩虹最小合约
    "RainbowMax"彩虹最大合约
  • 需要的合约参数：
  • "Expiration"到期日，或到期期限
    "StrikePrice"合约执行价格
  • FinancialDerivative 支持美式和欧式执行风格的彩虹最小与最大看涨看跌期权. 如果是美式执行风格，只支持一组资产中至多含有两种资产的情况.
  • 山脉范围期权（Mountain Range Option）
  • 山脉范围期权使持有者有权获得的支付基于一组资产在一定时间限制内的表现.
  • "Altiplano"Altiplano 山脉范围合约
    "Annapurna"Annapurna 山脉范围合约
    "Atlas"Atlas 山脉范围合约
    "Everest"Everest 山脉范围合约
    "Himalaya"Himalaya 山脉范围合约
  • 执行及期权类型的指定对于山脉范围期权来说不适用.
  • Altiplano 合约是这样一类山脉范围期权：如果这组资产中均没有达到其各自的障碍，则支付固定的息票额，否则支付为零.
  • Altiplano 合约的参数：
  • "Barriers"各资产的障碍值
    "Coupon"息票额
    "Expiration"到期日，或到期期限
  • Annapurna 合约在当资产均未降到各自的分数障碍价格时，支付固定的息票额，否则支付为零.
  • Annapurna 期权的参数：
  • "Fractions"触发有效条件的资产价格分数
    "Coupon"息票额
    "Expiration"到期日，或到期期限
  • Atlas 合约的支付基于除最好与最差资产外其它资产的表现.
  • Atlas 合约的参数：
  • "StrikePrice"期权执行价格，由一个乘积因子表示
    "NominalAmount"期权回报所累积的现金额
    "Expiration"到期日，或到期期限
  • Everest 合约的支付基于一组资产中最差资产的表现.
  • Everest 合约的参数：
  • "NominalAmount"期权回报所累积的现金额
    "Expiration"到期日，或到期期限
  • Himalaya 合约的支付基于逐渐减少的一组资产中最佳资产的表现. 到期期限被分为子期限，其中每一子期限内的收益由该期限内最佳资产的回报决定，并且用于决定子期回报的各资产被恰好使用一次.
  • Himalaya 合约的参数：
  • "NominalAmount"期权回报所累积的现金额
    "Expiration"到期日，或到期期限
  • 取差期权
  • 取差期权是一种多资产期权，其价值取决于到期日时标的资产的价差.
  • "Spread"两资产取差期权
  • 需要的合约参数：
  • "Expiration"到期日，或到期期限
    "StrikePrice"合约执行价格
  • FinancialDerivative 支持美式与欧式执行风格的取差看涨与看跌期权.
  • 汇率连动标准期权
  • 汇率连动标准期权在到期日的价值不仅取决于标的资产的表现，同时取决于控制该资产的货币的表现.
  • 期权名称：
  • "QuantoFixedExchange"固定汇率的汇率连动标准期权
    "QuantoFixedStrike"固定执行价格的汇率连动标准期权
  • 固定汇率的汇率连动标准期权在一个预先确定的汇率下结算. 固定执行价格的汇率连动标准期权在现行汇率下外币的固定执行价格下结算.
  • 需要的合约参数：
  • "Expiration"到期日，或到期期限
    "StrikePrice"合约执行价格
  • FinancialDerivative 支持美式与欧式执行风格的汇率连动标准看涨与看跌期权.

范例

打开所有单元关闭所有单元

基本范例  (6)

一个欧式看涨期权的价值：

一个欧式看涨期权的价值以及所有的 Greeks：

已知合约到期日，计算价值：

列出现有的所有合约类型：

列出所有 CUDA 加速的合约：

通过在列表中给出参数，利用 GPU 和并行计算最大限度地提高衍生品估值的性能：

范围  (30)

合约类型  (27)

标准式  (3)

确定一个标准合约的参数：

一个美式标准合约的价值：

计算一个美式标准合约与一个欧式标准合约的价值之差：

计算合约的隐含波动率：

亚式  (3)

计算一个亚式期权的价值：

该期权的价值与平均数的权重相关：

计算亚式算术认购期权的价值和 Greeks：

障碍式  (2)

计算一个障碍期权的价值：

与标准期权相比，障碍值限制期权持有者的正效益：

计算一个双重障碍出局期权的价值：

复合式  (3)

计算一个欧式执行看涨期权关于一个看涨期权的价值：

具有相同参数的可延期期权的价值要大于或等于复合式期权：

具有相同参数的选择式期权的价值要远比以上两者要昂贵：

回顾式  (3)

计算一个固定执行价格的回顾期权和一个浮动执行价格的回顾期权的 delta：

已知一个永久回顾看跌期权的临界值，求产生该临界值所需的波动率：

绘制该永久型期权临界值的波动率效果图：

幂式  (3)

计算标准欧氏幂式认购期权的价值：

计算欧氏幂式认沽期权的值：

计算欧氏封顶幂式认沽期权的值：

彩虹式  (5)

计算一个彩虹最佳期权的值：

计算彩虹最大认购期权的价值和 Greeks：

指定上三角形式的相关矩阵，以及作为公共值的股息与波动率：

一个彩虹货币期权是对所有资产组分不良表现的对冲：

绘制作为波动率函数的组合资产表现范围：

范围式  (5)

计算一个 Himalaya 合约的价值：

计算安那普那合约的 vega、theta 和 rho 数值：

范围合约价值是利用模拟计算的，并且受小型不确定性的影响：

回报执行价格为1的 Atlas 期权计算的是在指定名义额上累积的一组股票的正态化平均收益率：

由于回报在名义额上累加，当前资产价格并不重要：

日期  (3)

日期指定方式必须完全一致：

假定所有利率是在同一时间单位下，通常是年：

通过指定日利率也可得到相同价值：

选项  (12)

Method  (1)

利用非默认方法计算一个期权的价值：

"GridSize"  (2)

较短的到期期限要求在时间域上具有较少的网格点：

通过构建一个较细的空间网格提高对环境参数的敏感度：

"Paths"  (2)

更改一个基于模拟的求解程序的默认路径数：

将样本数翻为四倍使得误差减半：

"RuntimeTarget"(option available in Wolfram Finance Platform only)  (3)

默认情况下，选项设置 "RuntimeTarget"->Automatic 选择最快的可用运行时目标：

选项设置 "RuntimeTarget"->"CUDA" 强制运行时目标设置为具有 CUDA 功能的 GPU：

设置 "Device" 和 "TargetPrecision" 可以分别用于指定目标 CUDA 设备和所需精度：

一般情况下，设置 "TargetPrecision"->"Double" 可比 "TargetPrecision"->"Single" 设置生成精度更高的结果.

选项设置 "RuntimeTarget"->"Generic" 强制将运行时目标设为本地 CPU：

"Steps"  (3)

对于具有障碍的范围期权，增量参数确定对各路径采样的频率：

对于亚式期权，增量参数表示随各价格路径取平均数的次数：

控制二项树算法的步数：

"Caching"  (1)

对于篮子期权和亚式期权，Caching->True 对蒙特卡罗解决方法相关的数值进行缓存. 默认情况下， Caching->False:

应用  (3)

绘制一个看涨取差期权的回报率曲面：

将 Greeks 的值作为距到期日所剩时间的函数，绘制图形：

绘制一个美式看跌合约的临界值曲面：

属性和关系  (1)

通过绘制勒让德变换的图形，验证 delta 即是合约相对当前价格的敏感度：

可能存在的问题  (1)

默认的空间网格大小并不确保对一些参数的选项是正确的：

Wolfram Research (2010)，FinancialDerivative，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FinancialDerivative.html （更新于 2012 年）.

文本

Wolfram Research (2010)，FinancialDerivative，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FinancialDerivative.html （更新于 2012 年）.

CMS

Wolfram 语言. 2010. "FinancialDerivative." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2012. https://reference.wolfram.com/language/ref/FinancialDerivative.html.

APA

Wolfram 语言. (2010). FinancialDerivative. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FinancialDerivative.html 年

BibTeX

@misc{reference.wolfram_2024_financialderivative, author="Wolfram Research", title="{FinancialDerivative}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/FinancialDerivative.html}", note=[Accessed: 25-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_financialderivative, organization={Wolfram Research}, title={FinancialDerivative}, year={2012}, url={https://reference.wolfram.com/language/ref/FinancialDerivative.html}, note=[Accessed: 25-November-2024 ]}