FiniteFieldElementNorm
有限体の元 a の絶対ノルムを与える.
a の周辺体の ![]() 元部分体のと相対的な a のノルムを与える.
元部分体のと相対的な a のノルムを与える.
FiniteFieldElementNorm[a,emb]
有限体埋込み emb と相対的な a のノルムを与える.
詳細

- 標数が p で
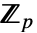 上の拡大次数が d の有限体
上の拡大次数が d の有限体 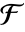 について,a の絶対ノルムは
について,a の絶対ノルムは 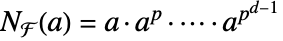 で与えられる.
で与えられる.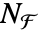 は
は 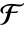 から
から 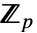 への写像で,
への写像で,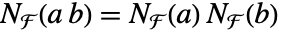 である.
である. - MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0なら
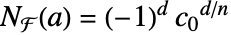 である.
である. - FiniteFieldElementNorm[a]は
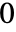 から
から 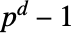 までの整数を与える.
までの整数を与える. - 標数 p,
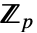 上の拡大次数 d の有限体
上の拡大次数 d の有限体 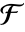 について,
について,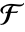 の
の 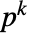 元部分体
元部分体 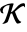 のと相対的な a のノルムは
のと相対的な a のノルムは 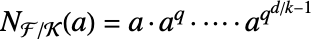 で与えられる.ただし,
で与えられる.ただし,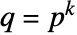 である.
である.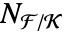 は
は 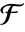 から
から 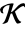 への写像で,
への写像で,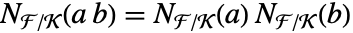 である.k は d の除数でなければならない.
である.k は d の除数でなければならない. - MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0なら
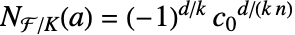 である.
である. - FiniteFieldElementNorm[a,k]は
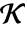 の元を与える.
の元を与える. - emb=FiniteFieldEmbedding[e1e2]ならFiniteFieldElementNorm[a,emb]は,事実上,emb["Projection"][FiniteFieldElementNorm[a,k]],を与える.ただし,a は e2の周辺体に属し,k は e1の周辺体の拡大次数である.
例題
すべて開くすべて閉じるスコープ (2)
特性と関係 (7)
FrobeniusAutomorphismを使って a の共役を計算する:
![]() が
が ![]() の
の ![]() 元の部分体なら,
元の部分体なら,![]() は乗算を保持する
は乗算を保持する ![]() から
から ![]() への写像である:
への写像である:
MinimalPolynomialを使って c と d は ![]() の
の![]() 元の部分体
元の部分体 ![]() に属することを示す:
に属することを示す:
FiniteFieldElementNormは移行性特性を満足する:
MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0なら ![]() である:
である:
MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0なら ![]() である:
である:
テキスト
Wolfram Research (2023), FiniteFieldElementNorm, Wolfram言語関数, https://reference.wolfram.com/language/ref/FiniteFieldElementNorm.html.
CMS
Wolfram Language. 2023. "FiniteFieldElementNorm." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FiniteFieldElementNorm.html.
APA
Wolfram Language. (2023). FiniteFieldElementNorm. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FiniteFieldElementNorm.html