gives the value of the Frobenius automorphism at the finite field element a.
gives the value of the kth functional power of the Frobenius automorphism at a.


FrobeniusAutomorphism
gives the value of the Frobenius automorphism at the finite field element a.
gives the value of the kth functional power of the Frobenius automorphism at a.
Details
- For a finite field
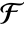 with characteristic
with characteristic 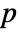 , the Frobenius automorphism is given by
, the Frobenius automorphism is given by 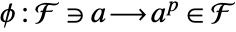 .
. - All finite field automorphisms are functional powers of the Frobenius automorphism.
- The number of different field automorphisms of
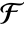 is equal to the extension degree of
is equal to the extension degree of 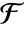 over
over 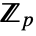 .
. - Any field automorphism
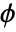 satisfies equations
satisfies equations 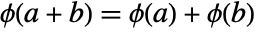 and
and 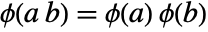 .
. - If n is the degree of the MinimalPolynomial f of an element a of
 , then Table[FrobeniusAutomorphism[a,k],{k,n}] gives all the roots of f in
, then Table[FrobeniusAutomorphism[a,k],{k,n}] gives all the roots of f in  .
.
Examples
open all close allBasic Examples (1)
Scope (1)
Applications (1)
Compute the minimal polynomial of an element of a finite field:
The minimal polynomial of ![]() is the product of
is the product of ![]() over all conjugates
over all conjugates ![]() of
of ![]() :
:
Convert to integer coefficients:
Compare with the result obtained using the built-in MinimalPolynomial:
Properties & Relations (5)
Frobenius automorphism is a field automorphism:
For a finite field ![]() with characteristic
with characteristic ![]() , the Frobenius automorphism is given by
, the Frobenius automorphism is given by ![]() :
:
All finite field automorphisms are functional powers of the Frobenius automorphism:
Use FiniteFieldEmbedding to find an automorphism of ![]() :
:
Identify the functional power of the Frobenius automorphism that gives the same mapping:
The number of different field automorphisms of ![]() is equal to the extension degree of
is equal to the extension degree of ![]() over
over ![]() :
:
Compute all conjugates of a finite field element a:
The absolute trace of a is equal to the sum of conjugates:
Use FiniteFieldElementTrace to compute the absolute trace:
The absolute norm of a is equal to the product of conjugates:
Use FiniteFieldElementNorm to compute the absolute norm:
The conjugates are roots of MinimalPolynomial[a]:
Related Guides
History
Text
Wolfram Research (2023), FrobeniusAutomorphism, Wolfram Language function, https://reference.wolfram.com/language/ref/FrobeniusAutomorphism.html.
CMS
Wolfram Language. 2023. "FrobeniusAutomorphism." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FrobeniusAutomorphism.html.
APA
Wolfram Language. (2023). FrobeniusAutomorphism. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FrobeniusAutomorphism.html
BibTeX
@misc{reference.wolfram_2025_frobeniusautomorphism, author="Wolfram Research", title="{FrobeniusAutomorphism}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/FrobeniusAutomorphism.html}", note=[Accessed: 22-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_frobeniusautomorphism, organization={Wolfram Research}, title={FrobeniusAutomorphism}, year={2023}, url={https://reference.wolfram.com/language/ref/FrobeniusAutomorphism.html}, note=[Accessed: 22-January-2026]}