FiniteFieldElementTrace
更多信息

- 对于在
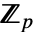 上具有特征 p 和扩张度 d 的有限域
上具有特征 p 和扩张度 d 的有限域 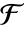 ,a 的绝对迹由
,a 的绝对迹由 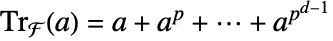 给出.
给出. 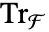 是从
是从 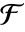 到
到 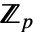 的
的 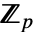 -线性映射.
-线性映射. - 如果 MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0,则
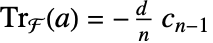 .
. - FiniteFieldElementTrace[a] 给出介于
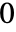 和
和 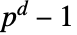 之间的整数.
之间的整数. - 对于在
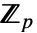 上具有特征 p 和扩张度 d 的有限域
上具有特征 p 和扩张度 d 的有限域 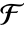 ,a 相对于
,a 相对于 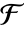 的
的 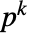 -元素子域
-元素子域 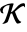 的迹由
的迹由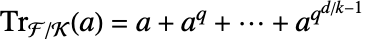 给出,其中
给出,其中 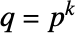 .
. 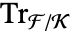 是从
是从 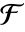 到
到 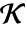 的
的 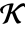 -线性映射. k 必须是 d 的约数.
-线性映射. k 必须是 d 的约数. - 如果 MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0,则
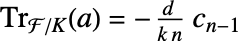 .
. - FiniteFieldElementTrace[a,k] 给出
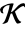 的元素.
的元素. - 如果 emb=FiniteFieldEmbedding[e1e2],则 FiniteFieldElementTrace[a,emb] 实际上给出 emb["Projection"][FiniteFieldElementTrace[a,k]],其中 a 属于 e2 的环境域,k 是 e1 的环境域的扩张度.
范例
打开所有单元关闭所有单元属性和关系 (7)
使用 FrobeniusAutomorphism 计算 a 的共轭:
使用 FiniteFieldEmbedding 在 ![]() 中嵌入一个
中嵌入一个 ![]() 元素域
元素域 ![]() :
:
FiniteFieldElementTrace 满足传递性:
如果 MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0,则 ![]() :
:
如果 MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0,则 ![]() :
:
Wolfram Research (2023),FiniteFieldElementTrace,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FiniteFieldElementTrace.html.
文本
Wolfram Research (2023),FiniteFieldElementTrace,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FiniteFieldElementTrace.html.
CMS
Wolfram 语言. 2023. "FiniteFieldElementTrace." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FiniteFieldElementTrace.html.
APA
Wolfram 语言. (2023). FiniteFieldElementTrace. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FiniteFieldElementTrace.html 年