FitRegularization
更多信息

- Fit 和 FindFit 通常寻找最小化 norm(res) 的参数 pars,其中 res 是残差向量,被定义为数据坐标点处的模型和数据响应之间的差. 当 FitRegularization->rfun 时,最小化的目标是 norm(residuals)+rfun(pars).
- Fit 和 FindFit 求能范数最小化
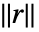 的参数
的参数  ,其中
,其中 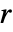 是残差向量,其分量由
是残差向量,其分量由 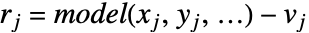 给出,其中
给出,其中 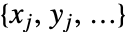 是数据的坐标,
是数据的坐标,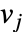 是数据的值,model 取决于参数.
是数据的值,model 取决于参数. - 可能的设置包括:
-
None 没有正则化 rfun 用 rfun[a] 正则化 {"Tikhonov", λ} 用 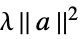 正则化
正则化{"LASSO",λ} 用 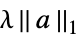 正则化
正则化{"Variation",λ} 用 ![lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||^2 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||^2](Files/FitRegularization.zh/9.png) 正则化
正则化{"TotalVariation",λ} 用 ![lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||_1 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||_1](Files/FitRegularization.zh/10.png) 正则化
正则化{"Curvature",λ} 用 ![lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a,2]||^2 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a,2]||^2](Files/FitRegularization.zh/11.png) 正则化
正则化{r1,r2,…} 用 r1,… 中各项的和正则化
范例
打开所有单元关闭所有单元应用 (5)
LinearSolve 求出的解含有非常大的项:

如果不使用正则化,预测的响应与信号非常接近,但是算出的输入有很多振荡:
如果使用 variation 正则化,可求出更加平滑的近似结果:
使用 total variation 正则化平滑带有跳变的损坏信号:
Wolfram Research (2019),FitRegularization,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FitRegularization.html.
文本
Wolfram Research (2019),FitRegularization,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FitRegularization.html.
CMS
Wolfram 语言. 2019. "FitRegularization." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FitRegularization.html.
APA
Wolfram 语言. (2019). FitRegularization. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FitRegularization.html 年