WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

FrobeniusAutomorphism

FrobeniusAutomorphism[a]

有限体の元 a におけるフロベニウス(Frobenius)自己同型の値を与える．

FrobeniusAutomorphism[a,k]

a におけるフロベニウス自己同型の各元を k 乗した値を与える．

詳細

標数が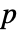の有限体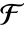について，フロベニウスの自己同型は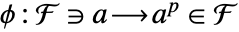で与えられる．
すべての有限体自己同型はフロヴェニウスの自己同型の各元の累乗である．
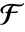の異なる体の自己同型の数は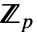上の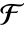の拡大次数に等しい．
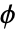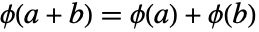任意の体の自己同型は方程式と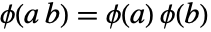を満足する．
n が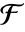の元 a のMinimalPolynomial f の次数なら，Table[FrobeniusAutomorphism[a,k],{k,n}]は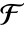における f のすべての根を与える．

例題

すべて開くすべて閉じる

例 (1)

標数，拡大次数の有限体を表す：

体の元におけるフロベニウス自己同型の値を計算する：

フロベニウス自己同型の関数の3乗：

スコープ (1)

フロベニウス自己同型の有限体の元における値を計算する：

a のすべての共役を計算する：

a の共役は a の最小多項式の根である：

アプリケーション (1)

有限体の元の最小多項式を計算する：

の最小多項式はのすべての共役に対するの積である：

整数係数に変換する：

組込みのMinimalPolynomialによる結果と比較する：

特性と関係 (5)

フロベニウス自己同型は体の自己同型である：

標数の有限体についてのフロベニウス自己同型はで与えられる：

有限体自己同型はすべてフロベニウス自己同型の関数乗である：

FiniteFieldEmbeddingを使っての自己同型を求める：

同じ写像を与えるフロベニウス自己同型の関数乗を特定する：

の異なる体の自己同型の数は上のの拡大次数に等しい：

有限体の元 a のすべての共役を計算する：

a の絶対トレースは共役の和に等しい：

FiniteFieldElementTraceを使って絶対トレースを計算する：

a の絶対ノルムは共役の積に等しい：

FiniteFieldElementNormを使って絶対ノルムを計算する：

共役はMinimalPolynomial[a]の根である：

トップへ