Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

FrobeniusAutomorphism

FrobeniusAutomorphism[a]

给出弗罗贝尼乌斯自同构在有限域元素 a 处的值.

FrobeniusAutomorphism[a,k]

给出弗罗贝尼乌斯自同构在 a 处的第 k 次泛函幂的值.

更多信息

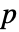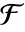对于特征为的有限域，弗罗贝尼乌斯自同构由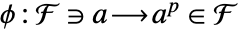给出.
所有有限域自同构都是弗罗贝尼乌斯自同构的泛函幂.
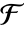的不同域自同构数等于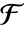在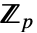上的扩张度.
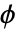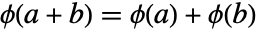任意域自同构满足方程和 .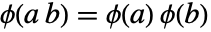
如果 n 是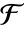的元素 a 的 MinimalPolynomial f 的次数，则 Table[FrobeniusAutomorphism[a,k],{k,n}] 给出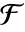中 f 的全部根.

范例

打开所有单元关闭所有单元

基本范例 (1)

表示具有特征和扩张度的有限域：

计算域元素的弗罗贝尼乌斯自同构值：

弗罗贝尼乌斯自同构的第三次泛函幂：

范围 (1)

计算有限域元素处的弗罗贝尼乌斯自同构值：

计算 a 的所有共轭：

a 的共轭是 a 的最小多项式的根：

应用 (1)

计算有限域元素的最小多项式：

的最小多项式是在的所有共轭上的乘积：

转换为整数系数：

与使用内置 MinimalPolynomial 获得的结果进行比较：

属性和关系 (5)

弗罗贝尼乌斯自同构是一个域自同构：

对于具有特征的有限域，弗罗贝尼乌斯自同构由给出：

所有有限域自同构都是弗罗贝尼乌斯自同构的泛函幂：

使用 FiniteFieldEmbedding 求的自同构：

识别给出相同映射的弗罗贝尼乌斯自同构的泛函幂：

的不同域自同构数等于在上的扩张度：

计算有限域元素 a 的所有共轭：

a 的绝对迹等于共轭的和：

使用 FiniteFieldElementTrace 计算绝对迹：

a 的绝对范数等于共轭的乘积：

使用 FiniteFieldElementNorm 计算绝对范数：

共轭是 MinimalPolynomial[a] 的根：

顶部