FrobeniusNumber

FrobeniusNumber[{a1,…,an}]

a1,…,anのフロベニウス(Frobenius)数を与える．

詳細

  • a1,…,anのフロベニウス数は，フロベニウス方程式 a1x1+…+anxn==b が非負の整数解を持たない最大の整数 b である．aiは正の整数でなければならない．
  • 整数 aiが互いに素でなければ，結果はInfinityになる．
  • aiのうちの1つが整数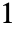のとき，結果は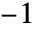になる．
  • b が a1,…,anのフロベニウス数のとき，FrobeniusSolve[{a1,…,an},b]は{}を返す．

例題

すべて開くすべて閉じる

例  (1)

12，16，20，27のフロベニウス数：

アプリケーション  (2)

フロベニウス数の配列を作る：

隣接する2数のフロベニウス数：

隣接する4数のフロベニウス数の場合を図示する：

特性と関係  (1)

互いに素である整数のペアについて，フロベニウス数は閉じた形を持つ：

検証する：

Wolfram Research (2007), FrobeniusNumber, Wolfram言語関数， https://reference.wolfram.com/language/ref/FrobeniusNumber.html.

テキスト

Wolfram Research (2007), FrobeniusNumber, Wolfram言語関数， https://reference.wolfram.com/language/ref/FrobeniusNumber.html.

CMS

Wolfram Language. 2007. "FrobeniusNumber." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FrobeniusNumber.html.

APA

Wolfram Language. (2007). FrobeniusNumber. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FrobeniusNumber.html

BibTeX

@misc{reference.wolfram_2024_frobeniusnumber, author="Wolfram Research", title="{FrobeniusNumber}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/FrobeniusNumber.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_frobeniusnumber, organization={Wolfram Research}, title={FrobeniusNumber}, year={2007}, url={https://reference.wolfram.com/language/ref/FrobeniusNumber.html}, note=[Accessed: 22-November-2024 ]}