



FullMoon
Details and Options

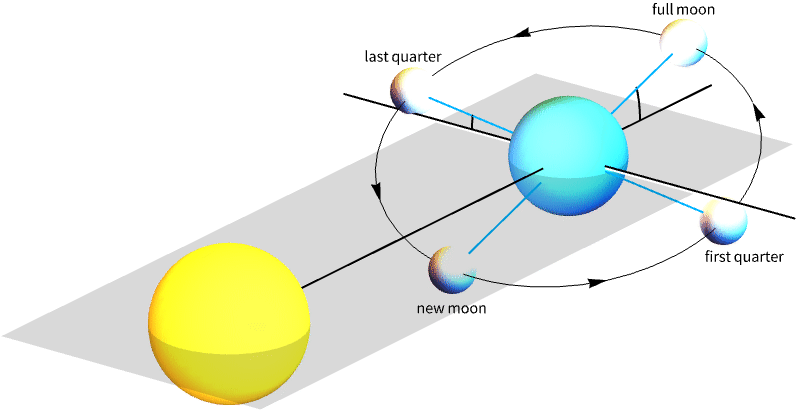
- The instant of full moon is defined by the opposition of the Moon and the Sun in ecliptic longitude.
- In FullMoon[date], date can be any DateObject expression.
- Options of FullMoon include:
-
CalendarType Automatic calendar used to return dates DateFormat Automatic format used to display output dates DateGranularity Automatic calendar granularity of output dates Method "EclipticLongitude" method to define moon phases TimeDirection 1 whether to return the next or last full moon TimeSystem Automatic time system of output dates TimeZone $TimeZone time zone of output dates - Possible settings for the Method option include:
-
"Illumination" phase defined by fraction of illumination of the Moon "EclipticLongitude" phase defined by Moon‐Sun ecliptic longitude difference
Examples
open all close allBasic Examples (2)
Scope (3)
Options (7)
CalendarType (1)
FullMoon returns dates in the Gregorian calendar by default:
DateFormat (1)
FullMoon returns dates in a long format by default:
DateGranularity (1)
FullMoon returns dates with granularity "Instant" by default:
Method (1)
FullMoon uses differences of ecliptic longitudes between the Sun and the Moon by default:
Use the minimum value of illumination to define the instant of new moon instead:
TimeDirection (1)
FullMoon finds the next full moon by default:
TimeSystem (1)
FullMoon returns dates in universal time by default:
TimeZone (1)
FullMoon returns dates in your local time zone by default:
Applications (1)
A full moon occurring near perigee, i.e. when the Moon is closest to Earth, is known as a supermoon.
Define a function computing the distance from the Earth to the Moon in kilometers:
Find all the full moons between years 2023 and 2026:
Plot distances during that period and mark the full moons as purple points:
The full moons occurring at smaller distances from Earth, say under 360,000 km, are the supermoons:
Properties & Relations (9)
At the instant of full moon, the Moon and the Sun have opposite ecliptic longitudes:
The distance between full moons varies between 29.26 and 29.80 days:
The average synodic month is about 29.53 days:
FullMoon returns the date of the next full moon:
Use NewMoon to find the date of the next new moon, which may be before or after that full moon:
Use MoonPhaseDate to find the date of any phase of the Moon:
MoonPhase computes the phase fraction of illumination, which is close to 1 for a full moon:
The maximum of illumination is given by this alternative method of computation:
This curve represents fraction of illumination for an hour around the maximum, with fullmoon in red:
Full moons correspond to semi-integer lunation numbers:
Therefore, an alternative way of finding full moons is calling FromLunationNumber with semi-integers:
FullMoon[date] is equivalent to FindAstroEvent["FullMoon",date]:
FullMoon defines Moon phases as observed from Earth's center:
This is also the default in FindAstroEvent:
FindAstroEvent will take parallax effects into account if an observer location is specified:
Full moons are oppositions of the Moon with respect to the Sun, as observed from the center of the Earth:
Every lunar eclipse happens within a few minutes of a full moon:
Only some of the 12 or 13 full moons in a year are close to lunar eclipses:
Related Guides
Text
Wolfram Research (2024), FullMoon, Wolfram Language function, https://reference.wolfram.com/language/ref/FullMoon.html (updated 2025).
CMS
Wolfram Language. 2024. "FullMoon." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/FullMoon.html.
APA
Wolfram Language. (2024). FullMoon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FullMoon.html
BibTeX
@misc{reference.wolfram_2025_fullmoon, author="Wolfram Research", title="{FullMoon}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/FullMoon.html}", note=[Accessed: 02-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_fullmoon, organization={Wolfram Research}, title={FullMoon}, year={2025}, url={https://reference.wolfram.com/language/ref/FullMoon.html}, note=[Accessed: 02-March-2026]}