is an option for FindSequenceFunction and related functions that specifies the space of functions to consider for representations.


FunctionSpace
is an option for FindSequenceFunction and related functions that specifies the space of functions to consider for representations.
Details
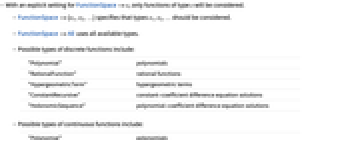
- With an explicit setting for FunctionSpace->s, only functions of type s will be considered.
- FunctionSpace->{s1,s2,…} specifies that types s1, s2, … should be considered.
- FunctionSpace->All uses all available types.
- Possible types of discrete functions include:
-
"Polynomial" polynomials "RationalFunction" rational functions "HypergeometricTerm" hypergeometric terms "ConstantRecursive" constant-coefficient difference equation solutions "HolonomicSequence" polynomial-coefficient difference equation solutions - Possible types of continuous functions include:
-
"Polynomial" polynomials "RationalFunction" rational functions "Hypergeometric" hypergeometric functions "HolonomicFunction" polynomial-coefficient differential equation solutions
Examples
Basic Examples (1)
By default, a small generating function is found if possible:
Use FunctionSpace to control the forms found:
History
Text
Wolfram Research (2008), FunctionSpace, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionSpace.html.
CMS
Wolfram Language. 2008. "FunctionSpace." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionSpace.html.
APA
Wolfram Language. (2008). FunctionSpace. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionSpace.html
BibTeX
@misc{reference.wolfram_2025_functionspace, author="Wolfram Research", title="{FunctionSpace}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionSpace.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_functionspace, organization={Wolfram Research}, title={FunctionSpace}, year={2008}, url={https://reference.wolfram.com/language/ref/FunctionSpace.html}, note=[Accessed: 09-March-2026]}