WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

GainPhaseMargins

GainPhaseMargins[lsys]

線形時不変系 lsys のゲイン余裕と位相余裕を与える．

詳細とオプション

系 lsys は，TransferFunctionModelまたはStateSpaceModelである．
GainPhaseMarginsは{{{ω_p₁,g₁},{ω_p₂,g₂},…},{{ω_g₁,p₁},{ω_g₂,p₂},…}}を返す．ただし，ω_piは位相交差周波数，g_iはゲイン余裕，ω_giはゲイン交差周波数，p_iは位相余裕である．
ゲイン余裕 g_iは絶対値であり位相余裕 p_iの単位はラジアンである．
ゲイン余裕は位相交差周波数における lsys の大きさの逆数である．
位相交差周波数での lsys の位相は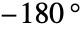である．
位相余裕はゲイン交差周波数で位相が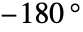になるための位相の遅れである．
位相交差周波数で，lsys のゲインは1である．
使用可能なオプション
FeedbackType "Negative" フィードバックの型

Method Automatic 使用するメソッド

SamplingPeriod None サンプリング周期
Methodオプションの明示的な設定値として"Solve"と"NSolve"がある．どちらの場合にも，SolveあるいはNSolveのメドッドをサブオプションとして指定することができる．デフォルト設定のAutomaticでは，lsys が厳密かどうかによってこれらのメソッドが切り換えられる．
GainPhaseMarginsは属性Listableを有する．

例題

すべて開くすべて閉じる

例 (1)

ある系のゲイン余裕と位相余裕：

スコープ (3)

複数の交差周波数を持つ系：

ゲイン交差周波数の数：

離散時間系：

時間遅延系の余裕：

一般化と拡張 (1)

GainPhaseMargins[TransferFunctionModel[g,var]]はGainPhaseMargins[g]と等価である：

オプション (2)

FeedbackType (2)

系は負のフィードバック系のループ伝達関数であるとみなされる：

系を正のフィードバック系の一部として指定する：

系を閉ループ系として指定する：

正のフィードバック系：

特性と関係 (2)

ゲイン余裕と位相余裕は全周波数応答プロットで可視化できる：

ゲイン余裕をデシベルで：

位相余裕を度で：

交差周波数の単位がラジアン/秒なら，次のようにこれをHzに変換できる：

StabilityMargins->Trueの設定でゲイン余裕と位相余裕を計算し描画する：

トップへ