WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

TransferFunctionModel
Copy to clipboard.
✖
TransferFunctionModel

Copy to clipboard.
✖

represents the model of the transfer-function matrix g[s] with complex variable s.

Copy to clipboard.
✖
TransferFunctionModel[{n[s],d[s]},s]

specifies the numerator n[s] and denominator d[s] of a transfer-function model.

Copy to clipboard.
✖

specifies the zeros z, poles p, and gain g of a transfer-function model.

Copy to clipboard.
✖

gives the transfer-function model of the systems model sys.

Details and Options

  • TransferFunctionModel is typically used for signal filters and control design.
  • A continuous-time system modeled by 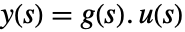where 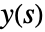is the Laplace transform of the output, 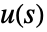is the Laplace transform of the input and 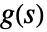is the transfer matrix can be specified as TransferFunctionModel[g[s],s].
    • Copy to clipboard.
    ✖
    https://wolfram.com/xid/0e490mxgkvo2hp-4nogqz
    Direct link to example
  • A discrete-time system modeled by 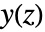where 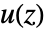is the Z transform of the output, 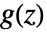is the Z transform of the input and 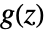is the transfer matrix can be specified as TransferFunctionModel[g[z],z,SamplingPeriodτ].
    • Copy to clipboard.
    ✖
    https://wolfram.com/xid/0e490mxgkvo2hp-8ndjdp
    Direct link to example
  • Time delays can be included in any transfer-function model, by using SystemsModelDelay.
  • In TransferFunctionModel[sys], the following systems can be converted:
  • AffineStateSpaceModelapproximate Taylor conversion
    NonlinearStateSpaceModelapproximate Taylor conversion
    StateSpaceModelexact conversion
  • The following options can be given:
  • MethodAutomaticthe method to obtain the transfer function of a state-space model
    SamplingPeriod Automaticthe sampling period of the system
    SystemsModelLabels Automaticlabels for the input and output variables
    ExternalTypeSignatureAutomaticvariable types for embedded code
  • Settings for the Method option include "DeterminantExpansion", "ResolventIdentities", "Inverse", and "Generic". With a setting Method->Automatic, the transfer-function model is computed using determinant expansion.

Examples

open allclose all

Basic Examples  (5)Summary of the most common use cases

A single-input, single-output system:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-lg83g1
Direct link to example
Out[1]=1

A system with two inputs and one output:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-1vrfvb
Direct link to example
Out[1]=1

Obtain the transfer-function representation of a state-space model:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-zsr5b1
Direct link to example
Out[1]=1

A discrete-time transfer function with a sampling period of 1:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-9loq7i
Direct link to example
Out[1]=1

Evaluate a transfer function over a range of frequencies:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-hl6m37
Direct link to example
Out[1]=1

Plot the magnitudes:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-l9hcpb
Direct link to example
Out[2]=2

Scope  (19)Survey of the scope of standard use cases

A first-order continuous-time system:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-bm0m6u
Direct link to example
Out[1]=1

A second-order system:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-crt0yr
Direct link to example
Out[1]=1

A fifth-order system:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-qxcu85
Direct link to example
Out[1]=1

A system with three zeros and six poles:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-ipocyf
Direct link to example
Out[1]=1

A first-order discrete-time system:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-uf959
Direct link to example
Out[1]=1

A two-input, one-output system:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-imjmvm
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-nkp2q3
Direct link to example
Out[2]=2

A one-input, two-output system:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-cmn0mc
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-b2xjo3
Direct link to example
Out[2]=2

A two-input, two-output system:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-gz8si0
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-e0klkb
Direct link to example
Out[2]=2

Specify a transfer function using its numerator and denominator:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-do1072
Direct link to example
Out[1]=1

A MIMO transfer function specified in terms of its numerators and denominators:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-xxuub9
Direct link to example
Out[1]=1

A denominator polynomial that is the least common multiple:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-766h15
Direct link to example
Out[1]=1

Specify the transfer function, using its algebraic poles, zeros, and gains:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-edricn
Direct link to example
Out[1]=1

A multivariable system:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-zxjo49
Direct link to example
Out[2]=2

A constant gain of 10:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-4q2pv3
Direct link to example
Out[1]=1

A discrete-time gain:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-wr1xmr
Direct link to example
Out[1]=1

A symbolic gain:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-l8f2xp
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-58tqpk
Direct link to example
Out[2]=2

The transfer-function representation of a state-space model:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-cmzziq
Direct link to example
Out[1]=1

Taylor linearize an AffineStateSpaceModel and obtain its transfer function representation:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-llm4k7
Direct link to example
Out[1]=1

The linearization of an AffineStateSpaceModel with nonzero equilibrium values:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-j8cp3e
Direct link to example
Out[2]=2

Taylor linearize a NonlinearStateSpaceModel:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-1st0aq
Direct link to example
Out[1]=1

The list of available properties:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-sdn80s
Direct link to example
Out[1]=1

Generalizations & Extensions  (2)Generalized and extended use cases

SISO systems can also be specified as a single-element list:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-fhnkqr
Direct link to example
Out[1]=1

Or just as a rational function:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-wsp05
Direct link to example
Out[2]=2

A single-output system can be given as a list:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-n02ouc
Direct link to example
Out[1]=1

Options  (5)Common values & functionality for each option

SamplingPeriod  (3)

Specify a continuous-time system:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-6rrmj
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-uaq3b3
Direct link to example
Out[2]=2

A discrete-time system with sampling period 1:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-eyx7sd
Direct link to example
Out[1]=1

A system with a symbolic sampling period:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-d04ii
Direct link to example
Out[1]=1

Set the sampling period to a numeric value:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-hi13zs
Direct link to example
Out[2]=2

SystemsModelLabels  (1)

Label the input and output variables:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-f6ffdo
Direct link to example
Out[1]=1

By default, the appearance is selected to fit the display in the notebook:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-yz4upi
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-b4ty5d
Direct link to example
Out[2]=2

Applications  (18)Sample problems that can be solved with this function

A proportional-integral (PI) controller:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-be2lf8
Direct link to example
Out[1]=1

A proportional-derivative (PD) controller:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-b4i0g7
Direct link to example
Out[1]=1

A function to construct a proportional-integral-derivative (PID) controller:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-p9a1fi
Direct link to example

A PID with specific gain values:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-3en2g8
Direct link to example
Out[2]=2

A function to construct a discrete-time PID controller:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-2arro8
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-358b5c
Direct link to example
Out[2]=2

A function for a continuous-time lead compensator:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-dyp1z5
Direct link to example

A lead compensator for specific values of gain and pole-zero locations:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-jktzhc
Direct link to example
Out[2]=2

A function for a continuous-time lag compensator:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-mcdxlc
Direct link to example

A specific lag compensator:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-66qlid
Direct link to example
Out[2]=2

A digital lag compensator defined in terms of its zero and pole locations:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-752klq
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-4x59v2
Direct link to example
Out[2]=2

A general formula for analog lowpass Butterworth filters:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-z375gh
Direct link to example

Filters of specific orders:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-mji7kr
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0e490mxgkvo2hp-w7jjpw
Direct link to example
Out[3]=3

A third-order Bessel filter:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-kektfk
Direct link to example
Out[1]=1

The general second-order transfer function:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-e37qx5
Direct link to example

Variations in damping ratio lead to qualitatively different responses:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-5hkq9n
Direct link to example

A linearized inverted pendulum model:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-ebckjx
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-m7ziil
Direct link to example
Out[2]=2

A spring-mass-damper system:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-cm5w7o
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-050nvv
Direct link to example
Out[2]=2

Transfer function between the input voltage and the shaft angular position of a DC motor:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-ylat3g
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-l5fkxy
Direct link to example
Out[2]=2

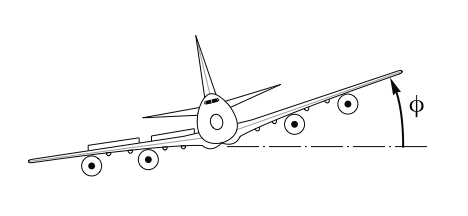
The aileron-to-roll-rate transfer function of an aircraft:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-qzfctt
Direct link to example
Out[1]=1

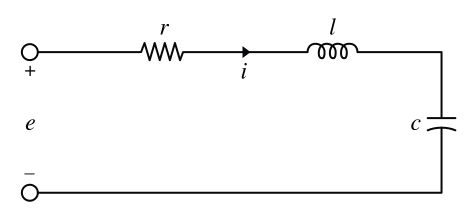
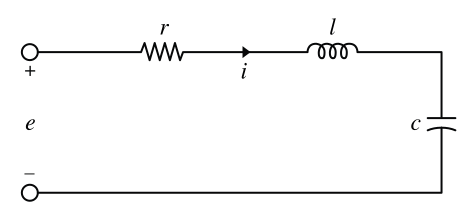
A temperature-controlled chemical reactor:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-phgygk
Direct link to example
Out[1]=1

An RLC circuit:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-5hahvv
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-ixhjcb
Direct link to example
Out[2]=2

A MIMO transfer function describing an aircraft's longitudinal dynamics:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-5k8k2a
Direct link to example
Out[1]=1

A ball mill grinding system with delay due to material transport:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-7bg0s
Direct link to example
Out[1]=1

Properties & Relations  (8)Properties of the function, and connections to other functions

TransferFunctionModel behaves as a pure function of one argument:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-0e8hmz
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-u501mo
Direct link to example
Out[2]=2

The value of the transfer-function matrix at a specific frequency:

Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0e490mxgkvo2hp-34ie7
Direct link to example
Out[3]=3

The values at several frequencies:

Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0e490mxgkvo2hp-ex2gfi
Direct link to example
Out[4]=4

Use TransferFunctionFactor to obtain the factored form:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-kyhtjx
Direct link to example
Out[1]=1

Obtain the expanded form:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-fg5dje
Direct link to example
Out[1]=1

Use TransferFunctionCancel to cancel any common poles and zeros:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-bymqys
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-1vvxu0
Direct link to example
Out[2]=2

Collect terms with similar powers:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-bfzoz1
Direct link to example
Out[1]=1

Collect terms in any variable:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-s3lpgk
Direct link to example
Out[1]=1

Find the element zeros and poles of a transfer-function matrix:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-vi61ey
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-8kgfuo
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0e490mxgkvo2hp-qns8tg
Direct link to example
Out[3]=3

Obtain a state-space form of a transfer-function model:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-q1jknm
Direct link to example
Out[1]=1

Possible Issues  (3)Common pitfalls and unexpected behavior

In TransferFunctionModel[m,var], pole-zero pairs may cancel before being processed:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-u09jrx
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-7m2bxy
Direct link to example
Out[2]=2

Use Unevaluated to prevent cancellations:

Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0e490mxgkvo2hp-3746b8
Direct link to example
Out[3]=3

Or use TransferFunctionModel[{num,den},var]:

Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0e490mxgkvo2hp-vjlq92
Direct link to example
Out[4]=4

Or TransferFunctionModel[{z,p,g},var]:

Copy to clipboard.
In[5]:=5
✖
https://wolfram.com/xid/0e490mxgkvo2hp-z3o5y4
Direct link to example
Out[5]=5

TransferFunctionModel[m,var] might result in a system with higher order:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-nui6rm
Direct link to example
Out[1]=1

Simplify the system:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-j4tm8r
Direct link to example
Out[2]=2

Or simplify m before passing it to TransferFunctionModel:

Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0e490mxgkvo2hp-chzkxi
Direct link to example
Out[3]=3
Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0e490mxgkvo2hp-dkwta3
Direct link to example
Out[4]=4

If the complex variable var is not specified, it is assumed to be s for continuous-time systems:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0e490mxgkvo2hp-hbdrjy
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0e490mxgkvo2hp-u83in2
Direct link to example
Out[2]=2

Specify the transfer function using s:

Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0e490mxgkvo2hp-3epe8h
Direct link to example
Out[3]=3

For discrete-time systems, use z:

Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0e490mxgkvo2hp-sc1qbq
Direct link to example
Out[4]=4
Wolfram Research (2010), TransferFunctionModel, Wolfram Language function, https://reference.wolfram.com/language/ref/TransferFunctionModel.html (updated 2014).
Copy to clipboard.
✖
Wolfram Research (2010), TransferFunctionModel, Wolfram Language function, https://reference.wolfram.com/language/ref/TransferFunctionModel.html (updated 2014).

Text

Wolfram Research (2010), TransferFunctionModel, Wolfram Language function, https://reference.wolfram.com/language/ref/TransferFunctionModel.html (updated 2014).

Copy to clipboard.
✖
Wolfram Research (2010), TransferFunctionModel, Wolfram Language function, https://reference.wolfram.com/language/ref/TransferFunctionModel.html (updated 2014).

CMS

Wolfram Language. 2010. "TransferFunctionModel." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/TransferFunctionModel.html.

Copy to clipboard.
✖
Wolfram Language. 2010. "TransferFunctionModel." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/TransferFunctionModel.html.

APA

Wolfram Language. (2010). TransferFunctionModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TransferFunctionModel.html

Copy to clipboard.
✖
Wolfram Language. (2010). TransferFunctionModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TransferFunctionModel.html

BibTeX

@misc{reference.wolfram_2025_transferfunctionmodel, author="Wolfram Research", title="{TransferFunctionModel}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/TransferFunctionModel.html}", note=[Accessed: 19-June-2025 ]}

Copy to clipboard.
✖
@misc{reference.wolfram_2025_transferfunctionmodel, author="Wolfram Research", title="{TransferFunctionModel}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/TransferFunctionModel.html}", note=[Accessed: 19-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_transferfunctionmodel, organization={Wolfram Research}, title={TransferFunctionModel}, year={2014}, url={https://reference.wolfram.com/language/ref/TransferFunctionModel.html}, note=[Accessed: 19-June-2025 ]}

Copy to clipboard.
✖
@online{reference.wolfram_2025_transferfunctionmodel, organization={Wolfram Research}, title={TransferFunctionModel}, year={2014}, url={https://reference.wolfram.com/language/ref/TransferFunctionModel.html}, note=[Accessed: 19-June-2025 ]}