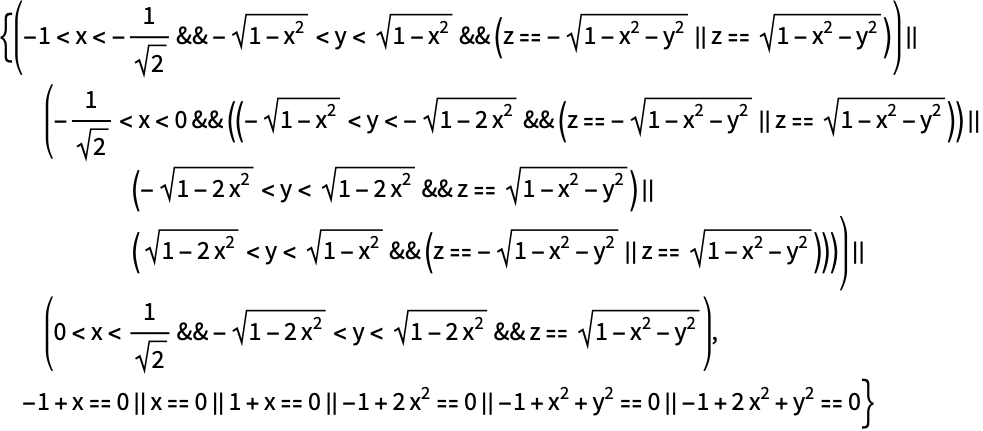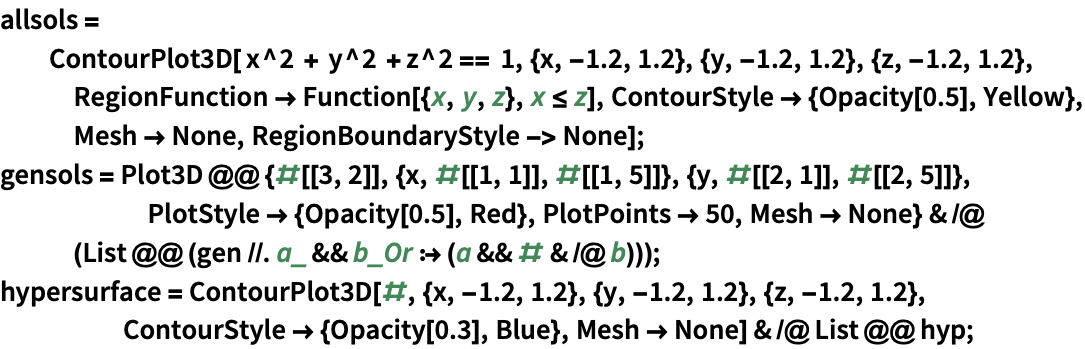WOLFRAM

Wolfram言語 ＆ システム ドキュメントセンター
Wolfram言語ホームページ »

GenericCylindricalDecomposition
✖
GenericCylindricalDecomposition

GenericCylindricalDecomposition[ineqs,{x1,x2,…}]

不等式 ineqs で表されている領域を，その方向が連続する xiに対応する円柱形の部分に分解したものの全次元の部分を，領域の残りを含む超曲面とともに求める．

詳細とオプション

例題

すべて開くすべて閉じる

例  (1)基本的な使用例

単位円板の全次元部分の円柱分解を求める：

In[1]:=1
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-g0n37k
Out[1]=1

スコープ  (3)標準的な使用例のスコープの概要

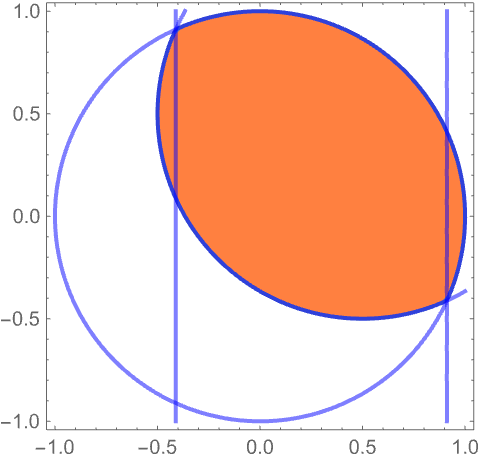
GenericCylindricalDecompositionは，全次元の解集合と超曲面を与える：

In[1]:=1
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-c96stz
In[2]:=2
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-ch9dy
Out[2]=2

超曲面はすべての解と全次元集合間の相違を含んでいる：

In[3]:=3
✖
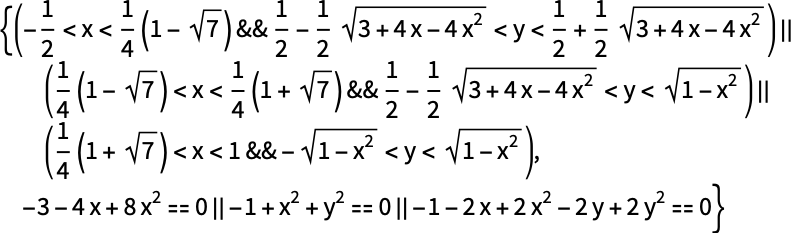
https://wolfram.com/xid/0tqhjt2hbnvqtu-dxzvpu
In[4]:=4
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-na0j2r
Out[4]=4

ここには超曲面は残っていない：

In[1]:=1
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-oeyhx
Out[1]=1

ここでは，解集合全体が低次元である：

In[1]:=1
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-cggm4j
Out[1]=1

一般化と拡張  (1)一般化および拡張された使用例

最初の2変数についての一般解を求める：

In[1]:=1
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-hpbrff
Out[1]=1

一般解と完全解の差は青い円柱曲面に含まれている：

In[2]:=2
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-6xxkk
In[3]:=3
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-gfmgji
Out[3]=3

オプション  (1)各オプションの一般的な値と機能

Method  (1)

デフォルトで，GenericCylindricalDecompositionは，等式と不等式の論理結合として表現される円柱分解を返す：

In[1]:=1
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-cf0dgm
Out[1]=1

Method{"CylindricalDecompositionFunctionOutput"True}を使ってCylindricalDecompositionFunctionの結果を得る：

In[2]:=2
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-7ufw6a
Out[2]=2

アプリケーション  (1)この関数で解くことのできる問題の例

不等式で表された範囲をプロットする：

In[1]:=1
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-cm2hyo
In[2]:=2
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-iw4udl
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-zav6h

曲面上の曲線は円柱境界に相当する：

In[4]:=4
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-bqra7n
Out[4]=4

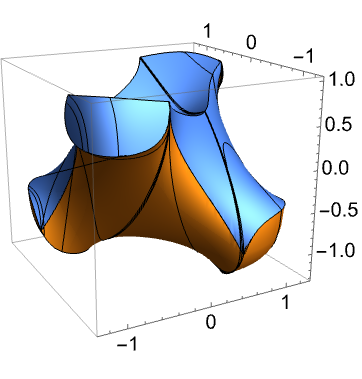
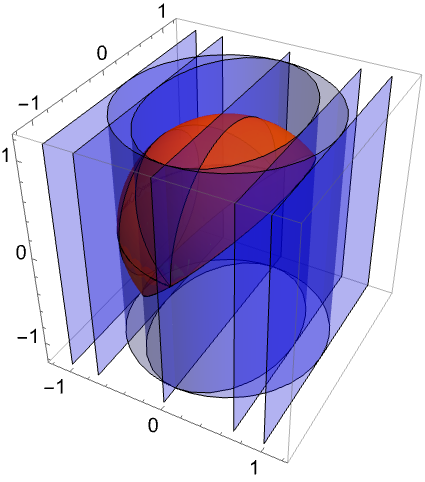
完全な円柱分解の計算にはより時間がかかり，画像のプロットには不要である：

In[5]:=5
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-bw9bj8
Out[5]=5

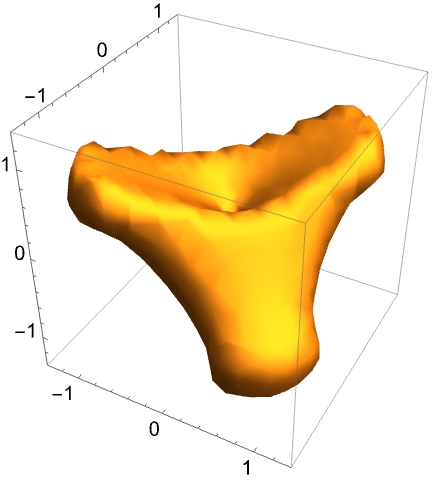
RegionPlot3Dは数値的な方法を使って若干精度に劣る画像を返す：

In[6]:=6
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-eouv4
Out[6]=6

特性と関係  (3)この関数の特性および他の関数との関係

GenericCylindricalDecompositionは低次元の部分までの解集合を求める：

In[1]:=1
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-lc34bd
Out[1]=1

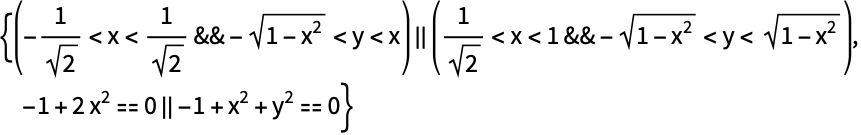
CylindricalDecompositionは完全な解集合を求める：

In[1]:=1
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-ha3x7s
Out[1]=1

Reduceは円柱分解を使って不等式を解く：

In[1]:=1
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-r8o3w
Out[1]=1

考えられる問題  (1)よく起る問題と予期しない動作

解集合の次元が低い場合には，解が求まらない：

In[1]:=1
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-v5yhu
Out[1]=1

低い次元の解集合を求めたければCylindricalDecompositionを使うとよい：

In[2]:=2
✖
https://wolfram.com/xid/0tqhjt2hbnvqtu-ezslgp
Out[2]=2
Wolfram Research (2007), GenericCylindricalDecomposition, Wolfram言語関数， https://reference.wolfram.com/language/ref/GenericCylindricalDecomposition.html.

テキスト

Wolfram Research (2007), GenericCylindricalDecomposition, Wolfram言語関数， https://reference.wolfram.com/language/ref/GenericCylindricalDecomposition.html.

CMS

Wolfram Language. 2007. "GenericCylindricalDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GenericCylindricalDecomposition.html.

APA

Wolfram Language. (2007). GenericCylindricalDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GenericCylindricalDecomposition.html

BibTeX

@misc{reference.wolfram_2025_genericcylindricaldecomposition, author="Wolfram Research", title="{GenericCylindricalDecomposition}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/GenericCylindricalDecomposition.html}", note=[Accessed: 03-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_genericcylindricaldecomposition, organization={Wolfram Research}, title={GenericCylindricalDecomposition}, year={2007}, url={https://reference.wolfram.com/language/ref/GenericCylindricalDecomposition.html}, note=[Accessed: 03-April-2025 ]}