CylindricalDecompositionFunction[data][x1,x2,…]
represents a cylindrical algebraic formula in x1,x2,….


CylindricalDecompositionFunction
CylindricalDecompositionFunction[data][x1,x2,…]
represents a cylindrical algebraic formula in x1,x2,….
Details and Options

- CylindricalDecompositionFunction[…][x1,x2,…] is generated by CylindricalDecomposition[expr, {x1,x2,…},"Function"].
- CylindricalDecompositionFunction objects provide an explicit compact representation of semialgebraic sets that can be efficiently used in further computation.
- CylindricalDecompositionFunction is typically used for repeated computations with semialgebraic sets, including computing Boolean combinations of sets, restricting sets with additional conditions, eliminating some variables or optimizing over sets.
- A cylindrical algebraic formula in x1,…,xn has the form
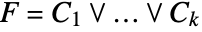 , where
, where 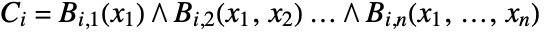 . Each
. Each 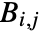 has the form either
has the form either 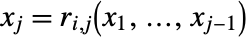 or
or 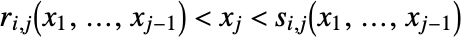 , where
, where 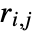 and
and 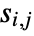 are algebraic functions that are defined and continuous on the solution set of
are algebraic functions that are defined and continuous on the solution set of 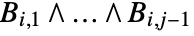 . The solution set
. The solution set 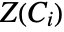 of
of 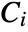 in
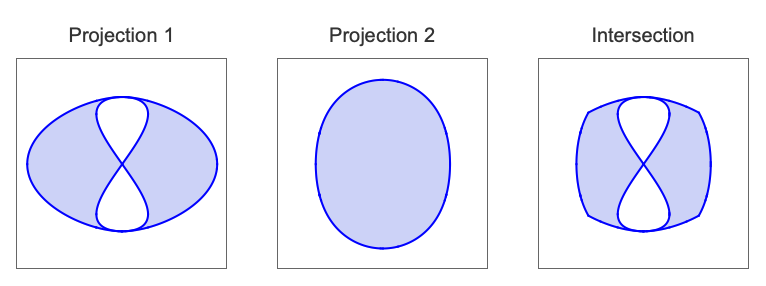
in 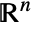 is called a cell. Projections of cells
is called a cell. Projections of cells 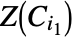 and
and 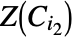 on
on 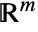 , for any
, for any 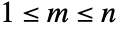 , are either disjoint or identical.
, are either disjoint or identical. - CylindricalDecompositionFunction provides an encapsulated representation of cylindrical algebraic formulas, which is often more efficient when used in the input to CylindricalDecompositionFunction or CylindricalDecomposition, or to solvers such as Reduce, Resolve, FindInstance, Solve or Minimize.
- Normal converts CylindricalDecompositionFunction objects to explicit Boolean combinations of equations and inequalities.
Examples
open all close allBasic Examples (2)
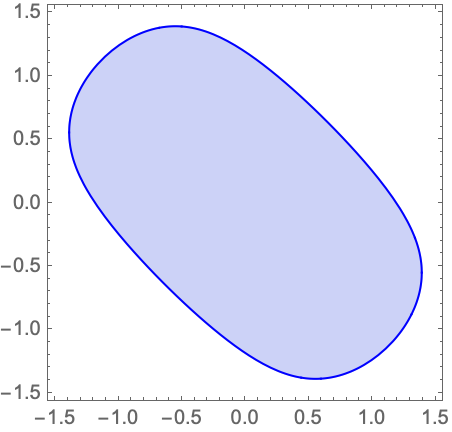
Find a cylindrical algebraic formula representation of the open unit ball:
Represent the single-cell solution as explicit inequalities:
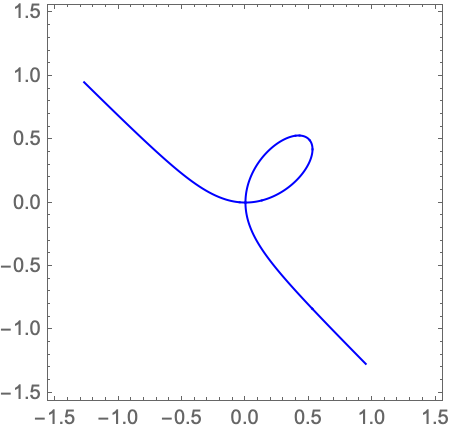
Find a cylindrical algebraic formula representation of the solution set of a quantified formula:
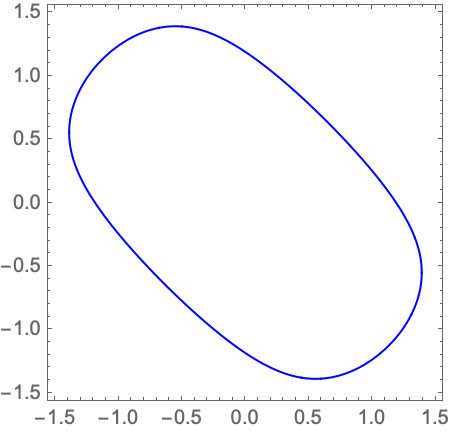
Compute the boundary of the solution set:
Scope (23)
Basic Uses (7)
Solution of polynomial equations and inequalities:
Coefficients can include real algebraic numbers:
Coefficients can include real exact transcendental numbers:
Solution of a quantified system of polynomial equations and inequalities:
CylindricalDecompositionFunction with a constant truth value simplifies to True or False:
CylindricalDecompositionFunction with real numeric initial arguments simplifies automatically:
Use CylindricalDecompositionFunction objects in further computation:
Compose a CylindricalDecompositionFunction with an algebraic mapping:
Use a Boolean combination of CylindricalDecompositionFunction objects and polynomial inequalities:
Boolean Operations (2)
Compute a CylindricalDecompositionFunction solution ![]() of a quantified system:
of a quantified system:
Compute CylindricalDecompositionFunction solutions of two different quantified systems:
Solving Equations and Inequalities (2)
Compute a CylindricalDecompositionFunction solution ![]() of a quantified system:
of a quantified system:
Solve an equation over the solution set of ![]() :
:
Solve a Boolean combination of CylindricalDecompositionFunction objects, equations and inequalities:
Quantifier Elimination (3)
Eliminate quantifiers from quantified CylindricalDecompositionFunction objects:
Eliminate quantifiers when the variables are quantified in the same order they appear in the formula:
Eliminate quantifiers from systems involving CylindricalDecompositionFunction objects:
The cost of quantifier elimination depends on the order of variables:
When the quantified variables appear in the formula after the free variables, elimination is fast:
Elimination of quantifiers from formulas constructed in a different variable order is much slower:
Topological Operations (5)
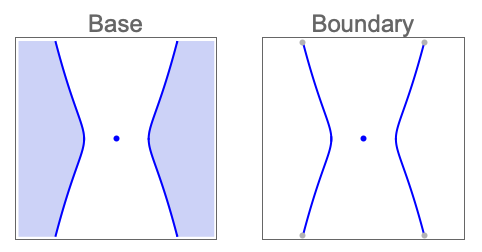
Find CylindricalDecompositionFunction representations of the solution region and its boundary:
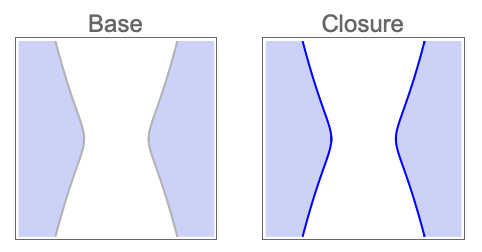
Find CylindricalDecompositionFunction representations of the solution region and its closure:
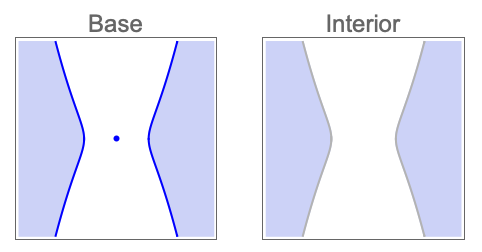
Find CylindricalDecompositionFunction representations of the solution region and its interior:
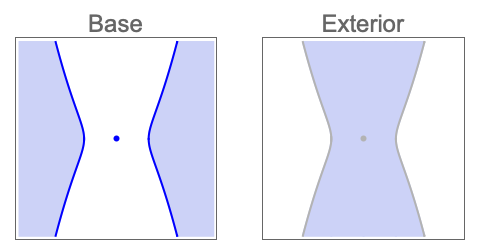
Find CylindricalDecompositionFunction representations of the solution region and its exterior:
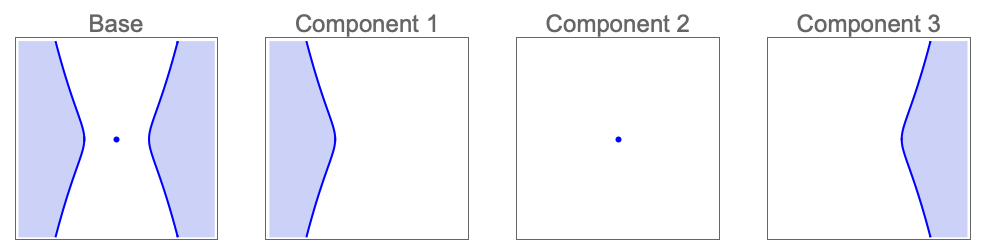
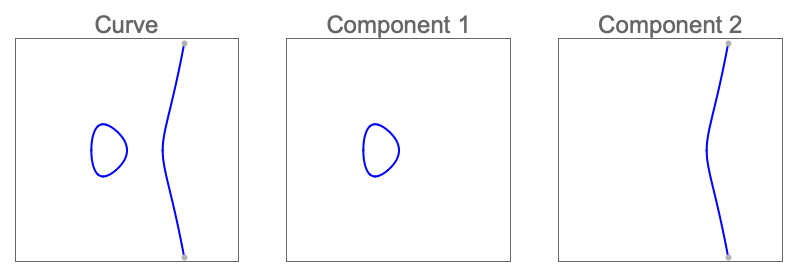
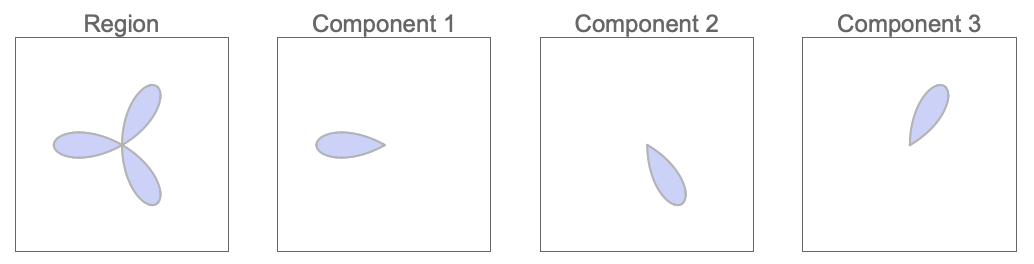
Find CylindricalDecompositionFunction representations of the solution region and its connected components:
CylindricalDecompositionFunction as Input to Solvers (4)
Use CylindricalDecompositionFunction to specify optimization constraints:
Solve systems involving equations, inequalities and CylindricalDecompositionFunction constraints:
Use FindInstance to find solution instances for systems involving CylindricalDecompositionFunction:
Find at least one point in each connected component of the solution set of a CylindricalDecompositionFunction:
Applications (4)
Properties & Relations (5)
This gives a cylindrical algebraic formula in an encapsulated form:
By default, CylindricalDecomposition gives the formula written as explicit equations and inequalities:
Normal of the CylindricalDecompositionFunction object is equivalent, and often identical, to the formula computed directly:
Cylindrical algebraic formulas in encapsulated form are often more efficient for further computation:
Operations on CylindricalDecompositionFunction objects are fast:
Operations on cylindrical algebraic formulas written as explicit equations and inequalities often are much slower:
Use FindInstance to find points that satisfy a CylindricalDecompositionFunction object:
SemialgebraicComponentInstances gives at least one point in each connected component of a semialgebraic set:
CylindricalDecompositionFunction merges several cells to get a more compact representation:
SemialgebraicComponentInstances now knows that fewer points suffice:
GenericCylindricalDecomposition computes representations of semialgebraic sets set up to lower-dimensional parts:
Use Method{"CylindricalDecompositionFunctionOutput"True} to get CylindricalDecompositionFunction results:
Possible Issues (1)
When given inexact arguments, CylindricalDecompositionFunction uses the inexact values of arguments for comparisons, but produces an exact result:
Related Guides
History
Text
Wolfram Research (2020), CylindricalDecompositionFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/CylindricalDecompositionFunction.html.
CMS
Wolfram Language. 2020. "CylindricalDecompositionFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CylindricalDecompositionFunction.html.
APA
Wolfram Language. (2020). CylindricalDecompositionFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CylindricalDecompositionFunction.html
BibTeX
@misc{reference.wolfram_2025_cylindricaldecompositionfunction, author="Wolfram Research", title="{CylindricalDecompositionFunction}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CylindricalDecompositionFunction.html}", note=[Accessed: 01-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_cylindricaldecompositionfunction, organization={Wolfram Research}, title={CylindricalDecompositionFunction}, year={2020}, url={https://reference.wolfram.com/language/ref/CylindricalDecompositionFunction.html}, note=[Accessed: 01-March-2026]}