GraphDistance

GraphDistance[g,s,t]

给出在图 g 中从源顶点 s 到目标顶点 t 的距离.

GraphDistance[g,s]

给出从 s 到图 g 中所有顶点的距离.

GraphDistance[{vw,…},…]

使用规则 vw 指定图 g.

更多信息和选项

  • GraphDistance 也被称为测地距离（geodesic distance）.
  • GraphDistance[g,s,t] 给出 s 和 t 之间的最短路径的长度.
  • 当 s 和 t 之间不存在路径时，距离为 Infinity.
  • 对于加权图，距离是 s 和 t 之间的任意路径上权值和的最小值.
  • 可以给出下列选项：
  • Method Automatic使用的方法
  • 可能的 Method 设置包括 "Dijkstra", "BellmanFord", 和 "UnitWeight".

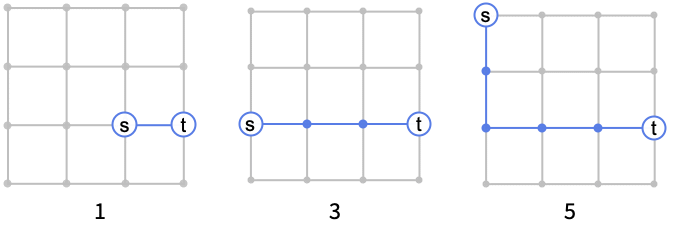
范例

打开所有单元关闭所有单元

基本范例  (1)

给出网格图的距离：

范围  (7)

GraphDistance 适用于无向图：

有向图：

加权图：

多图：

混合图：

使用规则指定图：

GraphDistance 适用于大规模图：

选项  (4)

Method  (4)

取决于输入，自动选择方法：

对于每条边，"UnitWeight" 方法将使用1作为权值：

"Dijkstra" 可以用于边的权值为正数的图：

"BellmanFord" 可被用于有向图，包括边权重为负值的情况：

应用  (5)

求大小为 {6,6} 的 GridGraph 的对角线之间的距离：

求大小为 {6,6,…,6} 的 -维 GridGraph 的对角之间的距离：

可视化一个树中从一个节点出发的距离：

获取从一个顶点到任意其它顶点的最大距离：

根据距离比例，设置颜色：

对概率为 的 Bernoulli 图，两个顶点之间的期望距离为 ：

在一个小字母表上，显示简短词汇的 DamerauLevenshteinDistance：

求两个单词之间的 Damerau–Levenshtein 距离：

检查结果：

属性和关系  (3)

两个顶点之间的距离可以使用 FindShortestPath 求得：

距离矩阵：

在连接图中，可用 GraphDistance 来计算 VertexEccentricity：

属于不同连通分量的两个顶点之间的距离是 Infinity:

Wolfram Research (2010)，GraphDistance，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GraphDistance.html （更新于 2015 年）.

文本

Wolfram Research (2010)，GraphDistance，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GraphDistance.html （更新于 2015 年）.

CMS

Wolfram 语言. 2010. "GraphDistance." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/GraphDistance.html.

APA

Wolfram 语言. (2010). GraphDistance. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GraphDistance.html 年

BibTeX

@misc{reference.wolfram_2024_graphdistance, author="Wolfram Research", title="{GraphDistance}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphDistance.html}", note=[Accessed: 24-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_graphdistance, organization={Wolfram Research}, title={GraphDistance}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphDistance.html}, note=[Accessed: 24-November-2024 ]}