WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

GraphDistanceMatrix
✖
GraphDistanceMatrix

✖

gives the matrix of distances between vertices for the graph g.

✖

gives the matrix of distances between vertices of maximal distance d in the graph g.

✖
GraphDistanceMatrix[{vw,…},…]

uses rules vw to specify the graph g.

Details and Options

  • GraphDistanceMatrix is also known as the shortest path matrix.
  • GraphDistanceMatrix returns a SparseArray object or an ordinary matrix.
  • The entries of the distance matrix dij give the shortest distance from vertex vi to vertex vj.
  • The diagonal entries dii of the distance matrix are always zero.
  • The entry dij is Infinity (∞) if there is no path from vertex vi to vertex vj.
  • In GraphDistanceMatrix[g,d], an entry dij will be Infinity if there is no path from vertex vi to vertex vj in d steps or less.
  • The vertices vi are assumed to be in the order given by VertexList[g].
  • For a weighted graph, the distance is the minimum of the sum of weights along any path from vertex vi to vertex vj.
  • The following options can be given:
  • EdgeWeightAutomaticweight for each edge
    Method Automaticmethod to use
  • Possible Method settings include "Dijkstra", "FloydWarshall", and "Johnson".

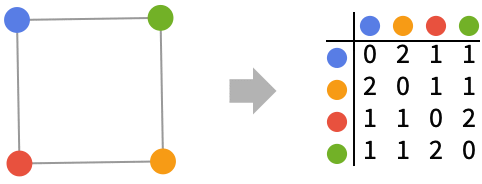
Examples

open allclose all

Basic Examples  (1)Summary of the most common use cases

Give the distance matrix for a Petersen graph:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-bjyzil

Scope  (8)Survey of the scope of standard use cases

GraphDistanceMatrix works with undirected graphs:

In[3]:=3
✖
https://wolfram.com/xid/0bniox635m7aa-6x5vth

Directed graphs:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-h8fgmr

Weighted graphs:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-zk71wo

Multigraphs:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-mqgkub

Mixed graphs:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-zc89h

Use rules to specify the graph:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-bndh30

Extract a single matrix column for a graph of modest size:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-i1la8a
Out[1]=1

Using GraphDistance to compute the same result takes more time:

In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-3crmlo
Out[2]=2

GraphDistanceMatrix works with large graphs:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-r64pi
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-x6vlgs
Out[2]=2

When just a single column is needed and the graph is large, using GraphDistance is faster:

In[3]:=3
✖
https://wolfram.com/xid/0bniox635m7aa-qteknj
Out[3]=3

Options  (6)Common values & functionality for each option

Method  (6)

The method is automatically chosen depending on input:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-bucy2s
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-wvbg31
Out[2]=2

"UnitWeight" method will use the weight 1 for every edge:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-y0asw2
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-4i73mg

"Dijkstra" can be used for graphs with positive edge weights only:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-d7080i
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-ifee4a

"FloydWarshall" can be used for directed graphs including negative edge weights:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-1m9g73
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-fgt3fm

"Johnson" can be used for directed graphs including negative edge weights:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-zlgrax
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-fmhs37

"Johnson" can be faster than the "FloydWarshall" method on sparse graphs:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-nzpa6
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-i6i3d0

Applications  (2)Sample problems that can be solved with this function

Find the vertex eccentricity, taking the entire graph into account:

In[6]:=6
✖
https://wolfram.com/xid/0bniox635m7aa-ldb7w8
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0bniox635m7aa-0j3xjv
Out[7]=7

For the strongly connected graph, the result is in agreement with VertexEccentricity:

In[8]:=8
✖
https://wolfram.com/xid/0bniox635m7aa-v44cwp
Out[8]=8

Find the vertex eccentricity of every vertex in a connected graph:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-r2py27
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-ujhopa
Out[2]=2

Check the result:

In[3]:=3
✖
https://wolfram.com/xid/0bniox635m7aa-1ldjkv
Out[3]=3

Properties & Relations  (5)Properties of the function, and connections to other functions

Rows and columns of the distance matrix follow the order given by VertexList:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-b9x6e
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-cwu88m
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bniox635m7aa-18iohr

The diagonal entries of the distance matrix are always zero:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-b0i77r
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-ev1mrp
Out[2]=2

The distance matrix can be found using GraphDistance:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-c04req
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-0wuo2a
Out[2]=2

In a connected graph, the VertexEccentricity can be obtained from the distance matrix:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-c9jm2d
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-ys095y
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bniox635m7aa-d9k98q
Out[3]=3

The distance between two vertices belonging to different connected components is Infinity:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-fs0db
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-col2m4
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bniox635m7aa-b8grwg

Possible Issues  (2)Common pitfalls and unexpected behavior

The matrix indices may not have the expected correspondence to vertices:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-b88rhv
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-z5zk77

The distance from 2 to 3 is not at the expected matrix position:

In[3]:=3
✖
https://wolfram.com/xid/0bniox635m7aa-x3cesy
Out[3]=3

The reason is that vertices are not in the expected order:

In[4]:=4
✖
https://wolfram.com/xid/0bniox635m7aa-u4zy75
Out[4]=4

Solve the problem by listing vertices explicitly when calling functions such as Graph:

In[6]:=6
✖
https://wolfram.com/xid/0bniox635m7aa-6i0gkf
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0bniox635m7aa-sl4xl2
Out[7]=7
In[8]:=8
✖
https://wolfram.com/xid/0bniox635m7aa-50fztd

Now the distance is found at the expected position:

In[9]:=9
✖
https://wolfram.com/xid/0bniox635m7aa-v09am0
Out[9]=9

"BellmanFord" is not a valid Method option:

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-ht2rtk
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-eacdeu

Use "FloydWarshall", "Johnson", or the default choice of Method instead:

In[3]:=3
✖
https://wolfram.com/xid/0bniox635m7aa-q56zfg
In[4]:=4
✖
https://wolfram.com/xid/0bniox635m7aa-r4f2bs
In[5]:=5
✖
https://wolfram.com/xid/0bniox635m7aa-7jftl1

Neat Examples  (1)Surprising or curious use cases

In[1]:=1
✖
https://wolfram.com/xid/0bniox635m7aa-rky9b
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bniox635m7aa-bk1h7z
Out[2]=2
Wolfram Research (2010), GraphDistanceMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html (updated 2015).
✖
Wolfram Research (2010), GraphDistanceMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html (updated 2015).

Text

Wolfram Research (2010), GraphDistanceMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html (updated 2015).

✖
Wolfram Research (2010), GraphDistanceMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html (updated 2015).

CMS

Wolfram Language. 2010. "GraphDistanceMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html.

✖
Wolfram Language. 2010. "GraphDistanceMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html.

APA

Wolfram Language. (2010). GraphDistanceMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html

✖
Wolfram Language. (2010). GraphDistanceMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html

BibTeX

@misc{reference.wolfram_2025_graphdistancematrix, author="Wolfram Research", title="{GraphDistanceMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html}", note=[Accessed: 31-May-2025 ]}

✖
@misc{reference.wolfram_2025_graphdistancematrix, author="Wolfram Research", title="{GraphDistanceMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html}", note=[Accessed: 31-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_graphdistancematrix, organization={Wolfram Research}, title={GraphDistanceMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html}, note=[Accessed: 31-May-2025 ]}

✖
@online{reference.wolfram_2025_graphdistancematrix, organization={Wolfram Research}, title={GraphDistanceMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html}, note=[Accessed: 31-May-2025 ]}