WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

HessenbergDecomposition

HessenbergDecomposition[m]

数値行列 m のヘッセンベルク(Hessenberg)分解を与える．

詳細とオプション

行列 m は正方形でなければならない．
結果は{p,h}の形で与えられる．ただし，h は上ヘッセンベルク行列で p はユニタリ行列であり， p.h.ConjugateTranspose[p]==m となる．
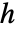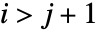上ヘッセンベルク行列は，のとき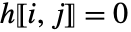を満足する．つまり，下対角の下のすべての成分は0である.
TargetStructure->"Structured"の設定のとき，HessenbergDecomposition[m]は行列{p,h}を構造化行列として返す．

例題

すべて開くすべて閉じる

例 (1)

4×4行列のヘッセンベルク分解を求める：

行列は上ヘッセンベルク行列である．このことは，この行列が最初の劣分対角の下にしか0を持たないことを意味する：

がユニタリ行列でであることを確認する：

スコープ (9)

基本的な用法 (5)

機械精度行列のヘッセンベルク分解を求める：

結果をフォーマットする：

複素行列のヘッセンベルク分解：

任意精度行列のヘッセンベルク分解：

厳密行列にHessenbergDecompositionを使う場合は，まず数値化しなければならない：

大きい数値行列のヘッセンベルク分解は効率的に計算される：

特殊行列 (4)

疎な行列のヘッセンベルク分解を求める：

構造化行列のヘッセンベルク分解：

恒等行列のヘッセンベルク分解は2つの恒等行列からなる：

HilbertMatrixのヘッセンベルク分解：

オプション (2)

TargetStructure (2)

実行列：

TargetStructure->"Dense"のとき，HessenbergDecompositionの結果は2つの密な行列のリストになる：

TargetStructure->"Structured"のとき．HessenbergDecompositionの結果はOrthogonalMatrixとSparseArrayを含むリストになる：

複素行列：

TargetStructure->"Dense"のとき，HessenbergDecompositionの結果は2つの密な行列のリストになる：

TargetStructure->"Structured"のとき，HessenbergDecompositionの結果はUnitaryMatrixとSparseArrayを含むリストになる：

アプリケーション (2)

ヘッセンベルク分解はエルミート行列に特に役に立つ．なぜなら，結果の行列が三重対角行列だからである．ランダムな6×6エルミート行列を生成する：

この行列がエルミート行列であることを確認する：

ヘッセンベルク分解を計算する：

小さい数値誤差を無視すれば，この行列は明らかに三重対角行列である：

行列が上ヘッセンベルク行列かつ下ヘッセンベルク行列なら，その行列は三重対角行列である．以下はChopで取り除いた小さい数が実際に数値的には重要ではなかったことを示している：

シューア(Schur)分解を計算する簡単な方法にシフトされていないQRアルゴリズムがある．から始めて各段階でのQR分解を計算し， $t_(k+1)=r.TemplateBox[{q}, Transpose]$ とする．極限では，は（正常に動作する入力行列については）希望する行列に収束する．速度を上げるためにこのアルゴリズムにを行列のヘッセンベルク分解の行列にするという変更を加える．非常に多くの項目がすでに0なので，各QR段階ははるかに速くなる．ランダムに生成された25×25実数対称行列についてこのことを見てみる：

行列は実対称行列である：

QRDecompositionを使ってシフトされていないQRアルゴリズムを2000回繰り返す：

の固有値は実数なので，それらは小さな数値誤差までの対角を構成する：

まずヘッセンベルク分解を計算する変更はおよそ2倍の速さである：

同時に，小さい数値誤差も生まれた：

特性と関係 (7)

乱数の4×4行列：

そのヘッセンベルク分解を計算する：

行列はユニタリ行列である：

行列は上ヘッセンベルク行列である：

もとの行列は，p.h.ConjugateTranspose[p]によって与えられる：

HessenbergDecomposition[h]は上ヘッセンベルク行列 h についてを返す：

2×2行列はどれも上ヘッセンベルク行列であり，HessenbergDecompositionを適用しても変更されずに返される：

Det[m]はHessenbergDecomposition[m]の行列の行列式に等しい：

Tr[m]はHessenbergDecomposition[m]の行列のトレースに等しい：

エルミート行列のヘッセンベルク分解は三重対角行列である：

ヘッセンベルク分解とシューア分解はどちらも実行列をヘッセンベルク行列に簡約する：

HessenbergDecompositionは行操作に基づいており，左上角は保持される：

SchurDecompositionは固有値に基づいている．対角下の成分は複素数値を示す：

考えられる問題 (1)

HessenbergDecompositionは，近似値の行列のみに使える：

厳密値の行列にはJordanDecompositionを使う：

トップへ