yields the Jordan decomposition of a square matrix m. The result is a list {s,j} where s is a similarity matrix and j is the Jordan canonical form of m.


JordanDecomposition
yields the Jordan decomposition of a square matrix m. The result is a list {s,j} where s is a similarity matrix and j is the Jordan canonical form of m.
Details

- The original matrix m is equal to s.j.Inverse[s]. »
- The matrix m can be either numerical or symbolic.
- The j matrix is called the Jordan normal form or Jordan canonical form.
- The Jordan normal form of a matrix is block diagonal with eigenvalues appearing by multiplicity on the main diagonal. The first superdiagonal can contain ones where there are nontrivial Jordan blocks from multiple eigenvalues. All other elements are zero.
- Each eigenvalue determines a block, and eigenvalues with multiplicity always appear together in the same block. They may be split into subblocks. A new subblock is indicated by not having a one above the eigenvalue, that is, in the position of the superdiagonal.
- The length of a block is the algebraic multiplicity of the eigenvalue. The number of subblocks is the geometric multiplicity and is the same as the dimension of the subspace spanned by linearly independent eigenvectors for that eigenvalue. This subspace is called the eigenspace for its eigenvalue.
- Each subblock is associated to a distinct eigenvector v from the eigenspace; taken together, these span that space. Subsequent vectors associated to a subblock are called generalized eigenvectors. For a matrix m and eigenvalue λ, the jth such vector vj is related to the true eigenvector of the subblock by the equation (m-λ imat)j.vj=v. Here imat is the identity matrix of the same size as m, and the exponent denotes the matrix power.
- The Jordan normal form is unique up to ordering of blocks and ordering of subblocks within blocks. Reorderings correspond to changes in the similarity matrices.
- When all eigenvalues have multiplicity 1, the Jordan normal form is the same up to ordering as the diagonal matrix comprised of those eigenvalues. This holds more generally when there are no ones on the superdiagonal, even if some eigenvalues have nontrivial multiplicity. In such cases, the similarity transformation is simply the transpose of the corresponding matrix of eigenvectors.
- Square matrices m1 and m2 with the same dimensions are said to be similar if there is an invertible matrix s of the same dimension such that m2=s.m1.Inverse[s]. Similar matrices have the same Jordan normal form.
Examples
open all close allScope (10)
Basic Uses (6)
Jordan decomposition of a machine-precision matrix:
Jordan decomposition of a complex matrix:
Jordan decomposition of an exact matrix with a deficient eigenspace:
The one in the third column of ![]() indicates that the eigenspace corresponding to 48 is deficient:
indicates that the eigenspace corresponding to 48 is deficient:
The third column of ![]() is therefore a generalized eigenvector where
is therefore a generalized eigenvector where ![]() gives
gives ![]() rather than
rather than ![]() :
:
Check that the decomposition correctly recovers the input matrix:
Jordan decomposition of an arbitrary-precision matrix:
Jordan decomposition of a symbolic matrix:
The Jordan decomposition of large numerical matrices is computed efficiently:
Special Matrices (4)
Jordan decomposition of sparse matrices:
Jordan decompositions of structured matrices:
IdentityMatrix is a Jordan canonical form:
The associated similarity matrix is a square root of the identity:
Jordan decomposition of a HilbertMatrix:
Applications (13)
Generalized Eigenvectors and Diagonalizability (4)
For the matrix ![]() , interpret the columns of the
, interpret the columns of the ![]() matrix of the Jordan decomposition in terms of true eigenvectors and generalized eigenvectors:
matrix of the Jordan decomposition in terms of true eigenvectors and generalized eigenvectors:
Compute the Jordan decomposition:
Columns of ![]() for which there is no
for which there is no ![]() above the diagonal in the corresponding of
above the diagonal in the corresponding of ![]() —columns 1, 3 and 4—are true eigenvectors for which
—columns 1, 3 and 4—are true eigenvectors for which ![]() :
:
The remaining column is a generalized eigenvector for which ![]() :
:
Show that the following matrix only has a single eigenvector, but it has a complete chain of generalized eigenvectors that form a basis for ![]() :
:
Eigensystem shows 84 is an eigenvalue of multiplicity 4 that has just one independent eigenvector:
The first column of the ![]() matrix of JordanDecomposition is the one eigenvector found:
matrix of JordanDecomposition is the one eigenvector found:
The remaining columns are a chain for which ![]() :
:
Since ![]() has an empty NullSpace, its columns form a basis for
has an empty NullSpace, its columns form a basis for ![]() :
:
A square matrix has a complete set of eigenvectors, and thus is diagonalizable, iff its ![]() matrix is diagonal:
matrix is diagonal:
Test if a particular matrix is diagonalizable:
Confirm using DiagonalizableMatrixQ:
Estimate the probability that a 4×4 matrix of ones and zeros will be diagonalizable:
An ![]() ×
×![]() matrix
matrix ![]() is nilpotent if
is nilpotent if ![]() for some
for some ![]() :
:
Consider a non-diagonalizable matrix ![]() :
:
![]() can be written as a sum of a diagonalizable matrix and a nilpotent matrix using JordanDecomposition:
can be written as a sum of a diagonalizable matrix and a nilpotent matrix using JordanDecomposition:
Let ![]() be the matrix formed from
be the matrix formed from ![]() and the diagonal part of
and the diagonal part of ![]() :
:
Let ![]() be the matrix formed from
be the matrix formed from ![]() and the superdiagonal part of
and the superdiagonal part of ![]() :
:
Similar Matrices (5)
A matrix m1 and a random invertible matrix s give a similar matrix m2:
The Jordan decomposition of m1:
The Jordan decomposition of m2:
Similar matrices share their Jordan form:
Since the eigenvalues are all distinct, the eigenvectors agree with the transpose of the similarity transform up to ordering and multiplication by constants:
For a diagonalizable matrix, the Jordan decomposition directly gives a diagonalization as ![]() . Apply this to diagonalize the matrix
. Apply this to diagonalize the matrix ![]() :
:
Compute the Jordan decomposition:
Let ![]() be the linear transformation whose standard matrix is given by the matrix
be the linear transformation whose standard matrix is given by the matrix ![]() . Find a basis
. Find a basis ![]() for
for ![]() with the property that the representation of
with the property that the representation of ![]() in that basis
in that basis ![]() is diagonal:
is diagonal:
Find the Jordan decomposition of ![]() :
:
Let ![]() consist of the eigenvectors, i.e the columns of
consist of the eigenvectors, i.e the columns of ![]() . As
. As ![]() converts from
converts from ![]() -coordinates to standard coordinates, its inverse converts in the reverse direction:
-coordinates to standard coordinates, its inverse converts in the reverse direction:
Thus ![]() is given by
is given by ![]() , which is diagonal:
, which is diagonal:
Note that this is simply the diagonal matrix whose entries are the eigenvalues:
A real-valued symmetric matrix ![]() is orthogonally diagonalizable as
is orthogonally diagonalizable as ![]() , with
, with ![]() diagonal and real valued and
diagonal and real valued and ![]() orthogonal. Verify that the following matrix is symmetric and then diagonalize it:
orthogonal. Verify that the following matrix is symmetric and then diagonalize it:
Compute the Jordan decomposition:
Let ![]() equal
equal ![]() after normalizing its columns:
after normalizing its columns:
Confirm that ![]() is indeed orthogonal:
is indeed orthogonal:
A matrix is called normal if ![]() . Normal matrices are the most general kind of matrix that can be diagonalized by a unitary transformation. All real symmetric matrices
. Normal matrices are the most general kind of matrix that can be diagonalized by a unitary transformation. All real symmetric matrices ![]() are normal because both sides of the equality are simply
are normal because both sides of the equality are simply ![]() :
:
Show that the following matrix is normal, then diagonalize it:
Confirm using NormalMatrixQ:
Compute the Jordan decomposition:
Unlike a real symmetric matrix, the diagonal matrix is complex valued:
Matrix Functions and Dynamical Systems (4)
Use the Jordan decomposition to compute ![]() and
and ![]() for the following matrix
for the following matrix ![]() :
:
Then ![]() . Since
. Since ![]() is upper triangular and nearly diagonal, the diagonal entries are raised to the power
is upper triangular and nearly diagonal, the diagonal entries are raised to the power ![]() , and the entry
, and the entry ![]() becomes
becomes ![]() :
:
Confirm with direct computation by MatrixPower:
Applying the power series for the exponential, the diagonal entries obviously become ![]() , and the off-diagonal term is merely a re-indexed exponential sum. Thus, it too becomes
, and the off-diagonal term is merely a re-indexed exponential sum. Thus, it too becomes ![]() :
:
Confirm using a direction computation by MatrixExp:
Confirm the formula 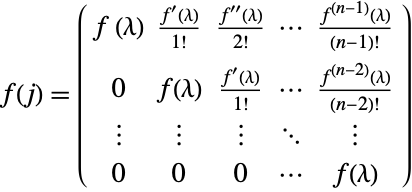 for a Jordan matrix consisting of a single chain for the following matrix
for a Jordan matrix consisting of a single chain for the following matrix ![]() and the functions
and the functions ![]() ,
, ![]() and
and ![]() :
:
First compute the formula for ![]() :
:
Verify the computation using MatrixFunction:
The computation for ![]() is analogous:
is analogous:
MatrixFunction confirms the result:
As ![]() has a parameter, it is necessary to use D instead of Derivative and substitute in
has a parameter, it is necessary to use D instead of Derivative and substitute in ![]() :
:
Again, MatrixFunction confirms the result when ![]() is entered using Function:
is entered using Function:
Solve the system of ODEs ![]() ,
, ![]() ,
, ![]() . First, construct the coefficient matrix
. First, construct the coefficient matrix ![]() for the right-hand side:
for the right-hand side:
Compute the Jordan decomposition of ![]() :
:
Using the formula of the previous example, ![]() is given by:
is given by:
The general solution is ![]() , for three arbitrary starting values:
, for three arbitrary starting values:
Verify the solution using DSolveValue:
Produce the general solution of the dynamical system ![]() when
when ![]() is the following stochastic matrix:
is the following stochastic matrix:
Compute the Jordan decomposition of ![]() :
:
Since the ![]() is diagonal,
is diagonal, ![]() consists of merely raising the diagonal entries to the power
consists of merely raising the diagonal entries to the power ![]() :
:
Properties & Relations (10)
JordanDecomposition[m] gives a matrix factorization of m as s.j.Inverse[s]:
Find the Jordan decomposition:
m is equal to s.j.Inverse[s]:
The eigenvalues of m are on the diagonal of j:
A matrix is diagonalizable iff the j matrix of its Jordan decomposition is diagonal:
EigenvalueDecomposition[m] exists if and only if m's Jordan matrix is diagonal:
The Jordan matrix of nd has a 1 above the diagonal:
When the decomposition exists, it agrees with JordanDecomposition:
As expected, the Jordan matrix is diagonal in this case:
For a diagonalizable matrix, JordanDecomposition reduces function application to application to eigenvalues:
Compute the matrix exponential using diagonalization, exponentiating only the diagonal entries:
Compute the matrix exponential using MatrixExp:
Note that this is not simply the exponential of each entry:
For a non-diagonalizable matrix, the Jordan decomposition restricts function application to each generalized eigenvector chain:
The j matrix is not diagonal, so m is not diagonalizable:
The function application only extends above the diagonal for columns for which j had a 1 above the diagonal:
For a real symmetric numerical matrix, the ![]() matrix is orthogonal:
matrix is orthogonal:
The ![]() matrix is diagonal and real valued:
matrix is diagonal and real valued:
For a real antisymmetric numerical matrix, the ![]() matrix is unitary:
matrix is unitary:
The ![]() matrix is diagonal with pure imaginary diagonal entries:
matrix is diagonal with pure imaginary diagonal entries:
For a real unitary numerical matrix, the ![]() matrix is unitary:
matrix is unitary:
The diagonal entries lie on the unit circle:
For a normal numerical matrix, the ![]() matrix is unitary:
matrix is unitary:
SchurDecomposition[n,RealBlockDiagonalFormFalse] for a numerical normal matrix ![]() :
:
Up to phase, this coincides with the Jordan decomposition:
The t and j matrices are equal:
To verify that q has eigenvectors as columns, set the first entry of each column to 1. to eliminate phase differences between q and s:
Possible Issues (2)
m is a 4×4 matrix with some entries differing by a small amount:
Find the Jordan decomposition using exact arithmetic:
This shows that m is diagonalizable:
Find the Jordan decomposition with machine‐number arithmetic:
Computation with machine-number arithmetic indicates that the matrix is not diagonalizable:
To machine precision, m is indistinguishable from a nearby non-diagonalizable matrix:
The matrix m has some machine-precision entries:
Due to numerical rounding, the deficient eigenspace at 2. is split into two separate eigenspaces:
Perform the computation using exact arithmetic to determine if the matrix is diagonalizable:
See Also
EigenvalueDecomposition Eigensystem JordanMatrix SingularValueDecomposition QRDecomposition SchurDecomposition MatrixExp MatrixFunction Minors
Function Repository: WeyrDecomposition
Tech Notes
Related Guides
History
Introduced in 1996 (3.0) | Updated in 2010 (8.0)
Text
Wolfram Research (1996), JordanDecomposition, Wolfram Language function, https://reference.wolfram.com/language/ref/JordanDecomposition.html (updated 2010).
CMS
Wolfram Language. 1996. "JordanDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2010. https://reference.wolfram.com/language/ref/JordanDecomposition.html.
APA
Wolfram Language. (1996). JordanDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JordanDecomposition.html
BibTeX
@misc{reference.wolfram_2025_jordandecomposition, author="Wolfram Research", title="{JordanDecomposition}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/JordanDecomposition.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_jordandecomposition, organization={Wolfram Research}, title={JordanDecomposition}, year={2010}, url={https://reference.wolfram.com/language/ref/JordanDecomposition.html}, note=[Accessed: 10-March-2026]}