WOLFRAM

Wolfram 语言与系统参考资料中心

HessenbergDecomposition[m]

给出数值矩阵 m 的 Hessenberg 分解.

更多信息和选项
Details and Options Details and Options
范例  
基本范例  
范围  
基础用法  
特殊矩阵  
选项  
TargetStructure  
应用  
属性和关系  
可能存在的问题  
参见
技术笔记
相关指南
历史
按以下格式引用：

HessenbergDecomposition

HessenbergDecomposition[m]

给出数值矩阵 m 的 Hessenberg 分解.

更多信息和选项

  • 矩阵 m 必须是方阵.
  • 结果以 {p,h} 的形式给出，其中 h 是上海森堡矩阵，p 是酉矩阵，使得 p.h.ConjugateTranspose[p]==m.
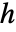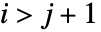  • 上海森伯格矩阵 满足 时 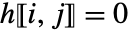的条件. 也就是说，其第一对角线以下的所有项都为零.
  • 设置 TargetStructure->"Structured"，HessenbergDecomposition[m] 以结构化矩阵的形式返回矩阵 {p,h}.

范例

打开所有单元 关闭所有单元

基本范例  (1)

找出 4×4 矩阵的海森伯格分解：

Wolfram Language code: m = (⁠| | | | | | :--- | :--- | :--- | :--- | | 1.0 | 2.9 | 3.8 | 4.7 | | 5.6 | 6.5 | 7.4 | 8.3 | | 9.2 | 10.1 | 11.0 | 12.9 | | 13.8 | 14.7 | 15.6 | 16.5 |⁠); {p, h} = HessenbergDecomposition[m]; {p//MatrixForm, h//MatrixForm}

矩阵 是上海森伯格矩阵，这意味着其在第一个下对角线下方只有零项：

Wolfram Language code: UpperTriangularMatrixQ[h, -1]

验证 为酉矩阵且 p.h.TemplateBox[{p}, ConjugateTranspose]=m：

Wolfram Language code: {UnitaryMatrixQ[p], p.h.p == m}

范围  (9)

基础用法  (5)

求机器精度矩阵的海森伯格分解：

Wolfram Language code: m = {{0.5, 0.3, 0.4}, {0.3, 1.1, -0.2}, {0.4, -0.2, 0.7}};
Wolfram Language code: {p, h} = HessenbergDecomposition[m]

格式化结果：

Wolfram Language code: MatrixForm /@ {p, h}

复矩阵的海森伯格分解：

Wolfram Language code: MatrixForm /@ HessenbergDecomposition[(⁠| | | | | ----------- | ----------- | ------------- | | 0.5 + 0.5 I | 1.1 | -1.3 - 3.3I | | -I | 3.2 - 4.5 I | -2.6 | | -2.3 + 1.2I | 0 | -1.3 + 0.24 I |⁠)]

任意精度矩阵的海森伯格分解：

Wolfram Language code: MatrixForm /@ HessenbergDecomposition[MatrixExp[RandomReal[1, {3, 3}, WorkingPrecision -> 12]]]

必须对精确矩阵进行数字化才能用于 HessenbergDecomposition：

Wolfram Language code: m = (⁠| | | | | -- | -- | -- | | 38 | 14 | 15 | | 14 | 35 | 8 | | 15 | 8 | 54 |⁠);
Wolfram Language code: HessenbergDecomposition[m]
Wolfram Language code: MatrixForm /@ HessenbergDecomposition[N[m]]

高效计算大型数值矩阵的海森伯格分解：

Wolfram Language code: mat = RandomReal[{0, 9}, {1000, 1000}];
Wolfram Language code: AbsoluteTiming[HessenbergDecomposition[mat];]

特殊矩阵  (4)

求稀疏矩阵的海森伯格分解：

Wolfram Language code: SparseArray[{{1, 1} -> 1.2, {1, 2} -> 2.1, {2, 2} -> 2, {2, 1} -> 0.5}, {2, 2}]
Wolfram Language code: HessenbergDecomposition[%]
Wolfram Language code: SparseArray[{{x_, y_} /; Abs[x - y] < 3 -> 1.5}, {5, 5}];
Wolfram Language code: MatrixForm /@ HessenbergDecomposition[%]

结构化矩阵的海森伯格分解：

Wolfram Language code: SymmetrizedArray[{{1, 1} -> 4.1, {2, 2} -> 3, {3, 1} -> 2, {3, 3} -> 1}, {3, 3}, Symmetric[All]]
Wolfram Language code: MatrixForm /@ HessenbergDecomposition[%]

单位矩阵的海森伯格分解由两个单位矩阵组成：

Wolfram Language code: {p, h} = HessenbergDecomposition[IdentityMatrix[3]//N]; Map[MatrixForm, {p, h}]

HilbertMatrix 的海森伯格分解：

Wolfram Language code: HessenbergDecomposition[HilbertMatrix[3]//N]; MatrixForm /@ %

选项  (2)

TargetStructure  (2)

实数矩阵：

Wolfram Language code: ma = RandomReal[1, {4, 4}]

设置 TargetStructure->"Dense"，则 HessenbergDecomposition 的结果是是两个稠密矩阵的列表：

Wolfram Language code: HessenbergDecomposition[ma, TargetStructure -> "Dense"]

设置 TargetStructure->"Structured"，则 HessenbergDecomposition 的结果是一个包含 OrthogonalMatrix 和 SparseArray 的列表：

Wolfram Language code: HessenbergDecomposition[ma, TargetStructure -> "Structured"]

复矩阵：

Wolfram Language code: ma = RandomComplex[1 + I, {4, 4}]

设置 TargetStructure->"Dense"，则 HessenbergDecomposition 的结果是两个稠密矩阵的列表：

Wolfram Language code: HessenbergDecomposition[ma, TargetStructure -> "Dense"]

设置 TargetStructure->"Structured"，则 HessenbergDecomposition 的结果是包含一个 UnitaryMatrix 和一个 SparseArray 的列表：

Wolfram Language code: HessenbergDecomposition[ma, TargetStructure -> "Structured"]

应用  (2)

海森伯格分解对于埃尔米特矩阵特别有用，因为生成的 矩阵是三对角矩阵. 生成一个随机的 6×6 埃尔米特矩阵：

Wolfram Language code: m = RandomVariate[GaussianSymplecticMatrixDistribution[3]]; Dimensions[m]

验证该矩阵为埃尔米特矩阵：

Wolfram Language code: HermitianMatrixQ[m]

计算海森伯格分解：

Wolfram Language code: {p, h} = HessenbergDecomposition[m];

若忽略小的数值误差，矩阵显然是三对角矩阵：

Wolfram Language code: Chop[MatrixForm[h]]

若某矩阵同时是上海森伯格和下海森伯格矩阵，则该矩阵为三对角矩阵. 以下显示了 Chop 丢弃的小数实际上为数值不显著：

Wolfram Language code: UpperTriangularMatrixQ[h, -1] && LowerTriangularMatrixQ[h, 1]

计算舒尔分解的一种简单方法是未移位 QR 算法. 从 开始，在每个阶段计算 的 QR 分解 ，然后令 t_(k+1)=r.TemplateBox[{q}, Transpose]. 在极限下， 收敛到所需的 矩阵（对于表现良好的输入矩阵）. 加速这个算法的一个修改是让 成为海森伯格分解的 矩阵. 因为这么多项都已经为零，所以每个 QR 步骤都快得多. 探索随机生成的 25×25 实对称矩阵：

Wolfram Language code: m = RandomVariate[GaussianOrthogonalMatrixDistribution[25]];

矩阵 为实值且对称矩阵：

Wolfram Language code: m∈ℝ && SymmetricMatrixQ[m]

使用 QRDecomposition 对未移位的 QR 算法进行 2000 次迭代：

Wolfram Language code: AbsoluteTiming[t = m;Do[{q, r} = QRDecomposition[t];t = r.Transpose[q], {2000}]]

由于 的特征值是实数，其构成了 的对角线，直到小数值误差：

Wolfram Language code: Norm[Sort[Diagonal[t]] - Sort[Eigenvalues[m]]]

首先计算的海森伯格分解的修改速度大约是原来的两倍：

Wolfram Language code: AbsoluteTiming[{p, h} = HessenbergDecomposition[m];Do[{q, r} = QRDecomposition[h];h = r.Transpose[q], {2000}]]

其也产生较小的数值误差：

Wolfram Language code: Norm[Sort[Diagonal[h]] - Sort[Eigenvalues[m]]]

属性和关系  (7)

随机 4×4 矩阵：

Wolfram Language code: m = RandomReal[{0, 1}, {4, 4}];

计算它的海森伯格分解：

Wolfram Language code: {p, h} = HessenbergDecomposition[m];

矩阵 是单模的：

Wolfram Language code: UnitaryMatrixQ[p]

矩阵 是上海森伯格矩阵：

Wolfram Language code: UpperTriangularMatrixQ[h, -1]

初始矩阵 由 p.h.ConjugateTranspose[p] 给出：

Wolfram Language code: p.h.ConjugateTranspose[p] - m//Chop

对于上海森伯格 矩阵 h，HessenbergDecomposition[h] 返回 ：

Wolfram Language code: h = UpperTriangularize[RandomReal[1, {10, 10}], -1]; {IdentityMatrix[10], h} == HessenbergDecomposition[h]

所有 2×2 矩阵都是上海森伯格矩阵，因此 HessenbergDecomposition 的返回不变：

Wolfram Language code: HessenbergDecomposition[(⁠| | | | --- | ---- | | 1.5 | -2.5 | | 3.5 | 4.5 |⁠)]

Det[m] 等于 HessenbergDecomposition[m] 的 矩阵的行列式：

Wolfram Language code: m = RandomReal[1, {5, 5}]; {p, h} = HessenbergDecomposition[m]; Det[m] == Det[h]

Tr[m] 等于 HessenbergDecomposition[m] 的 矩阵的迹：

Wolfram Language code: m = RandomReal[1, {5, 5}]; {p, h} = HessenbergDecomposition[m]; Tr[m] == Tr[h]

埃尔米特矩阵的海森伯格分解是三对角矩阵：

Wolfram Language code: m = RandomVariate[GaussianUnitaryMatrixDistribution[5]]; h = Last[HessenbergDecomposition[m]]; {HermitianMatrixQ[m], UpperTriangularMatrixQ[h, -1] && LowerTriangularMatrixQ[h, 1]}

海森伯格和舒尔分解都将实矩阵简化为海森伯格矩阵：

Wolfram Language code: m = (⁠| | | | | --- | ---- | --- | | 1.5 | -2.5 | 0.5 | | 3.5 | 4.5 | 0.5 | | 0.5 | 1.5 | 3.5 |⁠); {q, t} = SchurDecomposition[m]; {r, h} = HessenbergDecomposition[m]; {UpperTriangularMatrixQ[t, -1], UpperTriangularMatrixQ[h, -1]}

HessenbergDecomposition 基于行运算并保留左上角：

Wolfram Language code: h[[1, 1]] == m[[1, 1]]

SchurDecomposition 基于特征值；对角线下方的项表示复数值：

Wolfram Language code: t[[1, 1]] + Sqrt[t[[1, 2]]t[[2, 1]]]
Wolfram Language code: Eigenvalues[m][[2]]

可能存在的问题  (1)

HessenbergDecomposition 仅仅对近似数值矩阵有效：

Wolfram Language code: HessenbergDecomposition[{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}]

对精确矩阵使用 JordanDecomposition：

Wolfram Language code: JordanDecomposition[{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}]
Wolfram Research (2004)，HessenbergDecomposition，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HessenbergDecomposition.html （更新于 2024 年）.

文本

Wolfram Research (2004)，HessenbergDecomposition，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HessenbergDecomposition.html （更新于 2024 年）.

CMS

Wolfram 语言. 2004. "HessenbergDecomposition." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/HessenbergDecomposition.html.

APA

Wolfram 语言. (2004). HessenbergDecomposition. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HessenbergDecomposition.html 年

BibTeX

@misc{reference.wolfram_2026_hessenbergdecomposition, author="Wolfram Research", title="{HessenbergDecomposition}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/HessenbergDecomposition.html}", note=[Accessed: 03-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_hessenbergdecomposition, organization={Wolfram Research}, title={HessenbergDecomposition}, year={2024}, url={https://reference.wolfram.com/language/ref/HessenbergDecomposition.html}, note=[Accessed: 03-November-2026]}