HigmanSimsGroupHS
表示希格曼·西姆斯（Higman–Sims）散在单群 
.
背景
- HigmanSimsGroupHS[] 表示希格曼·西姆斯群
，是阶数为 ![TemplateBox[{2, 9}, Superscript].TemplateBox[{3, 2}, Superscript].TemplateBox[{5, 3}, Superscript].7.11](Files/HigmanSimsGroupHS.zh/3.png "TemplateBox[{2, 9}, Superscript].TemplateBox[{3, 2}, Superscript].TemplateBox[{5, 3}, Superscript].7.11")
的群. 它是 26 个有限阶散在单群之一. HigmanSimsGroupHS 的默认表示是作为有两个生成元的符号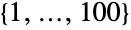 
上的置换群. - 希格曼·西姆斯群
是第 7 小的散在有限单群. 由数学家唐纳德·希曼（Donald G. Higman）和查尔斯·西姆斯（Charles Sims）在 20 世纪 60 年代末提出. HigmanSimsGroupHS 是所谓希格曼·西姆斯图的自同构群的单指数-2 子群并包含同构于马提厄群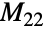 
的一点稳定子. 另外，除了各种置换表示，
可根据生成元和关系定义为 
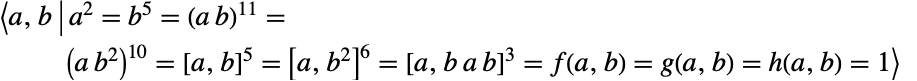，其中
, 
，
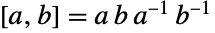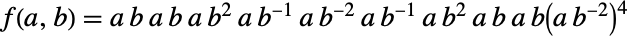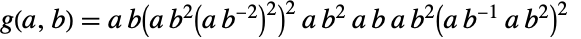和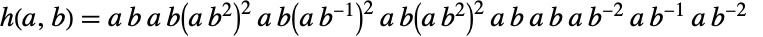
. 也可以作为各种置换群，例如 ConwayGroupCo2 和 ConwayGroupCo3 的子群，与所谓的利奇格（Leech lattice）相关. 与其他散在单群一起，
在有限单群的重大（和完全）分类中扮演基础角色. - 一般的群理论函数可应用于 HigmanSimsGroupHS[]，包括 GroupOrder、GroupGenerators、GroupElements 等. 然而，由于它的大型阶数，这些群理论函数可能返回未被计算的结果. 希格曼·西姆斯群群的预计算属性数值可以通过 FiniteGroupData["HigmanSims","prop"].
- HigmanSimsGroupHS 与其他符号有关. HigmanSimsGroupHS 是 7 个（其他是 ConwayGroupCo1, ConwayGroupCo2、ConwayGroupCo3、JankoGroupJ2、McLaughlinGroupMcL 和 SuzukiGroupSuz) “第二代”散在有限单群之一. 它也是 20 个所谓的“快乐”散群之一，它们都出现在魔群的子商中.
范例
Wolfram Research (2010)，HigmanSimsGroupHS，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HigmanSimsGroupHS.html.
文本
Wolfram Research (2010)，HigmanSimsGroupHS，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HigmanSimsGroupHS.html.
CMS
Wolfram 语言. 2010. "HigmanSimsGroupHS." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/HigmanSimsGroupHS.html.
APA
Wolfram 语言. (2010). HigmanSimsGroupHS. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HigmanSimsGroupHS.html 年