HumanGrowthData

HumanGrowthData[spec]

returns the range of values within one standard deviation of the mean for all properties of human growth at the specification spec.

HumanGrowthData[spec,property]

returns the range of values within one standard deviation of the mean of a property for the specification spec.

HumanGrowthData[spec,index]

returns the values for all properties of human growth for spec at the specified percentile.

HumanGrowthData[spec,property,index]

returns the value at a specific index of a property for spec at the specified percentile.

HumanGrowthData[spec,property,quantity]

returns the percentile and probability density for a specific value quantity of the property at spec.

Details and Options

  • The specification spec is an Association of the form Association["Age"->age,"Gender"->gender].
  • Age can be given as a positive Quantity of time or as a birth date using DateObject.
  • Data is not available for all ages. Human growth data is not available over the age of 20 years old.
  • Gender can be given as "Male" or "Female". It can also be the appropriate gender Entity.
  • If gender is not specified, then an Association with results for both "Male" and "Female" is returned.
  • Available properties include:
  • "BMI"body mass index
    "HeadCircumference"widest circumference of the head
    "Height"length as measured standing
    "Length"length as measured lying down
    "Milestones"typical developmental milestones reached around this age
    "NextMilestones"next milestones to expect
    "PreviousMilestones"milestones immediately proceeding this age
    "Weight"weight
  • The percentile index can be used to obtain the values of a property for a specified percentile in the distribution of a person with the specified gender and age.
  • The percentile index can be either a percentage Quantity between 0 and 100 percent or a number between 0 and 1, both exclusive. It can also be specified as an Association with the key "Percentage" or "ZScore". "ZScore" allows the value at a specific z-score, or number of standard deviations, from the mean (at 0). Z-score should be specified as a number between 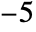and .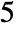
  • If no index is specified for an indexed property, the interval within a standard deviation of the mean is returned.
  • When a property is not specified, values for all properties will be returned as an Association with the properties as keys.
  • quantity should be a Quantity object and have compatible units for the property in question.
  • HumanGrowthData[spec,property,"StandardDeviation"] returns the StandardDeviation for that specification and property combination.
  • HumanGrowthData[spec,property,"Distribution"] returns a distribution for the specification and property combination, either a LogNormalDistribution for weight or a NormalDistribution.
  • HumanGrowthData[spec,property,"QuantityDistribution"] returns a QuantityDistribution for the specification and property combination, containing either a LogNormalDistribution for weight or a NormalDistribution.
  • HumanGrowthData takes the options:
  • Method Automaticdetermine model used
    UnitSystem $UnitSystemreturn units of the desired unit system
  • Method contains the suboption "Model", which allows you to specify the model to use. Available models include "CDC" and "WHO".
  • The "CDC" model uses data from the Centers for Disease Control and Prevention, http://www.cdc.gov/growthcharts. The "WHO" model uses data from the WHO Multicentre Growth Reference Study Group.

Examples

open allclose all

Basic Examples  (1)

Find the typical spectrum of lengths for four-month-old girls:

Discover the 50^(th) percentile weight for a young boy:

Scope  (9)

Learn the properties of HumanGrowthData:

Discover the values for all properties for a specified age and gender:

Use DateObject to specify birth dates:

Find the value of head circumference at the 80^(th) percentile:

Specify percentile as a fraction:

Use the z-score index to find the height of a child one standard deviation up from the mean:

Obtain the percentile and probability density for a particular length of a four-month-old girl:

Find the standard deviation for the weight of a 10-year-old boy:

Discover the distribution for the head circumference of an eight-month-old girl:

Obtain the QuantityDistribution instead:

Examine typical developmental milestones at a specific age:

Explore what milestones are coming up:

Options  (2)

Method  (1)

Choose to use the date either from the World Health Organization (WHO) or from the CDC:

UnitSystem  (1)

Control whether results are returned in metric or imperial units:

Applications  (8)

Explore percentile charts:

Examine the distribution of heights among full-grown men:

Find the probability a given man is six feet tall or taller:

Discover how the weight of males and females diverges over time:

Examine the ranges of male and female weights from to standard deviation over time:

Find the mean value for BMI and compare it to the median:

Examine how much extracellular water a full-grown person in the 50^(th) percentile of weight and height has, using the formula derived in Peters (2004):

Discover where various sports figures stand in the weight distribution chart for full-grown men:

Plot various actresses on a height distribution chart for full-grown women:

Explore how CDC and WHO data differs:

Properties & Relations  (1)

Use FetalGrowthData to examine average weight prior to birth and HumanGrowthData for the following year:

Possible Issues  (4)

Only dates prior to the present are acceptable birth dates:

Properties are only supported for a certain range of ages:

Data for all properties extends only to 20 years old:

Percentiles must be within the range 0 to 100, not including 0 or 100:

Probability density values are not available for all Quantity values:

Neat Examples  (5)

Show how weight distribution is not truly normal:

Fit to a LogNormalDistribution:

Examine how growth velocity changes with age:

Compare the growth acceleration for height and weight:

Approximate the bivariate stature‐weight distribution through a multinomial distribution of stature and the logarithm of weight and a correlation :

Typical correlation coefficients are about 0.45:

Generate 50,000 random samples of 20‐year-old females:

To learn why BMI is defined as weight/height^2, examine the correlation between the sample heights and a selection of possible combinations of weight and height:

For , the correlation between height and weight/height^alpha becomes minimal:

Plot a histogram of the BMI distribution:

Explore the timing of various physical milestones:

Wolfram Research (2015), HumanGrowthData, Wolfram Language function, https://reference.wolfram.com/language/ref/HumanGrowthData.html (updated 2018).

Text

Wolfram Research (2015), HumanGrowthData, Wolfram Language function, https://reference.wolfram.com/language/ref/HumanGrowthData.html (updated 2018).

CMS

Wolfram Language. 2015. "HumanGrowthData." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2018. https://reference.wolfram.com/language/ref/HumanGrowthData.html.

APA

Wolfram Language. (2015). HumanGrowthData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HumanGrowthData.html

BibTeX

@misc{reference.wolfram_2024_humangrowthdata, author="Wolfram Research", title="{HumanGrowthData}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/HumanGrowthData.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_humangrowthdata, organization={Wolfram Research}, title={HumanGrowthData}, year={2018}, url={https://reference.wolfram.com/language/ref/HumanGrowthData.html}, note=[Accessed: 22-December-2024 ]}