WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

IndependentVertexSetQ[g,vlist]

頂点リスト vlist がグラフ g 中の独立頂点集合であればTrueを，そうでなければFalseを返す．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
アプリケーション  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

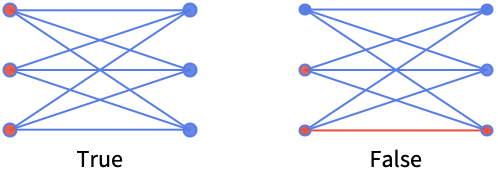
IndependentVertexSetQ

IndependentVertexSetQ[g,vlist]

頂点リスト vlist がグラフ g 中の独立頂点集合であればTrueを，そうでなければFalseを返す．

詳細

  • 独立頂点集合とは決して同じ辺に接続しない頂点集合のことである．
  • IndependentVertexSetQは，無向グラフ，有向グラフ，多重グラフ，混合グラフに使うことができる．

例題

すべて開く すべて閉じる

例  (2)

頂点集合が独立頂点集合かどうか調べる：

Wolfram Language code: IndependentVertexSetQ[[image], {1, 4}]

グラフ中のすべての頂点集合が独立頂点集合である訳ではない：

Wolfram Language code: IndependentVertexSetQ[[image], {1, 4}]

スコープ  (5)

無向グラフを調べる：

Wolfram Language code: IndependentVertexSetQ[[image], {2, 3, 4}]

有向グラフ：

Wolfram Language code: IndependentVertexSetQ[[image], {2, 3, 4}]

多重グラフ：

Wolfram Language code: IndependentVertexSetQ[[image], {2, 3, 4}]

混合グラフ：

Wolfram Language code: IndependentVertexSetQ[[image], {2, 3, 4}]

IndependentVertexSetQは大きいグラフに使うことができる：

Wolfram Language code: g = GridGraph[{10, 10, 10, 10}];
Wolfram Language code: IndependentVertexSetQ[g, {1, 2}]//Timing

アプリケーション  (2)

巡回グラフのすべての独立頂点集合を列挙する：

Wolfram Language code: g = CycleGraph[4, VertexSize -> Small]

頂点のすべての部分集合を列挙しその中から独立頂点集合を選ぶ：

Wolfram Language code: Subsets[VertexList[g]]
Wolfram Language code: vcl = Select[%, IndependentVertexSetQ[g, #]&]

独立頂点集合をハイライトする：

Wolfram Language code: Table[HighlightGraph[g, h], {h, vcl}]

ペテルセン(Petersen)グラフのすべての最大独立頂点集合を列挙する：

Wolfram Language code: g = PetersenGraph[5, 2, VertexSize -> Medium]

最大独立頂点集合の大きさを求める：

Wolfram Language code: FindIndependentVertexSet[g]
Wolfram Language code: n = Length[%]

すべての最大独立頂点集合を列挙する：

Wolfram Language code: vsl = Select[Subsets[VertexList[g], {4}], IndependentVertexSetQ[g, #]&]

最大独立頂点集合をハイライトする：

Wolfram Language code: Table[HighlightGraph[g, h], {h, vsl}]

特性と関係  (4)

最大独立頂点集合はFindIndependentVertexSetで求められる：

Wolfram Language code: PetersenGraph[5, 2]
Wolfram Language code: IndependentVertexSetQ[%, First[FindIndependentVertexSet[%]]]

独立頂点集合の補集合は頂点被覆である：

Wolfram Language code: g = GridGraph[{2, 3}]
Wolfram Language code: Complement[VertexList[%], First[FindIndependentVertexSet[%]]]
Wolfram Language code: VertexCoverQ[g, %]

独立頂点集合で与えられる補部分グラフは完全グラフである：

Wolfram Language code: g = PetersenGraph[5, 2]
Wolfram Language code: Subgraph[GraphComplement[g], FindIndependentVertexSet[g]]
Wolfram Language code: CompleteGraphQ[%]

二部グラフには長さが等しい辺被覆と独立頂点集合がある：

Wolfram Language code: g = CompleteGraph[{2, 3}]
Wolfram Language code: Length[First[FindIndependentVertexSet[g]]] == Length[FindEdgeCover[g]]
Wolfram Research (2010), IndependentVertexSetQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/IndependentVertexSetQ.html （2014年に更新）.

テキスト

Wolfram Research (2010), IndependentVertexSetQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/IndependentVertexSetQ.html （2014年に更新）.

CMS

Wolfram Language. 2010. "IndependentVertexSetQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/IndependentVertexSetQ.html.

APA

Wolfram Language. (2010). IndependentVertexSetQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/IndependentVertexSetQ.html

BibTeX

@misc{reference.wolfram_2026_independentvertexsetq, author="Wolfram Research", title="{IndependentVertexSetQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/IndependentVertexSetQ.html}", note=[Accessed: 01-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_independentvertexsetq, organization={Wolfram Research}, title={IndependentVertexSetQ}, year={2014}, url={https://reference.wolfram.com/language/ref/IndependentVertexSetQ.html}, note=[Accessed: 01-November-2026]}