InhomogeneousPoissonProcess[λ[t],t]
t の関数として与えられる強度が λ[t]の,非同次ポアソン(Poisson)過程を表す.


InhomogeneousPoissonProcess
InhomogeneousPoissonProcess[λ[t],t]
t の関数として与えられる強度が λ[t]の,非同次ポアソン(Poisson)過程を表す.
詳細
- InhomogeneousPoissonProcessは,連続時間・離散状態の過程である.
- 時点 t におけるInhomogeneousPoissonProcessは,区間0から t までの事象数である.
- 区間0から t までの事象数は,平均が
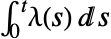 のPoissonDistributionに従う.
のPoissonDistributionに従う. - InhomogeneousPoissonProcessの定義中の強度関数 λ[t]は,有効であると仮定される.特に,連続する,正の値を持つ t の関数であると仮定される.
- InhomogeneousPoissonProcessは,Mean,PDF,Probability,RandomFunction等の関数とともに使うことができる.
例題
すべて開く すべて閉じるスコープ (10)
過程スライス特性 (5)
アプリケーション (3)
特性と関係 (3)
InhomogeneousPoissonProcessはジャンプ過程である:
一定強度の非同次ポアソン過程はPoissonProcessである:
考えられる問題 (1)
関連するガイド
テキスト
Wolfram Research (2015), InhomogeneousPoissonProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html.
CMS
Wolfram Language. 2015. "InhomogeneousPoissonProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html.
APA
Wolfram Language. (2015). InhomogeneousPoissonProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html
BibTeX
@misc{reference.wolfram_2025_inhomogeneouspoissonprocess, author="Wolfram Research", title="{InhomogeneousPoissonProcess}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html}", note=[Accessed: 02-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_inhomogeneouspoissonprocess, organization={Wolfram Research}, title={InhomogeneousPoissonProcess}, year={2015}, url={https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html}, note=[Accessed: 02-February-2026]}