InhomogeneousPoissonProcess[λ[t],t]
表示非齐次泊松过程,其中强度 λ[t] 是 t 的函数.


InhomogeneousPoissonProcess
InhomogeneousPoissonProcess[λ[t],t]
表示非齐次泊松过程,其中强度 λ[t] 是 t 的函数.
更多信息
- InhomogeneousPoissonProcess 是一个连续时间离散状态的过程.
- InhomogeneousPoissonProcess 在时间 t 是区间 0 到 t 的事件数.
- 区间 0 到 t 间的事件数遵循带有均值
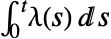 的 PoissonDistribution.
的 PoissonDistribution. - InhomogeneousPoissonProcess 定义中的强度函数 λ[t] 被假设为有效的. 尤其是,它被认为是 t 的连续的、正值函数.
- InhomogeneousPoissonProcess 可与函数 Mean、PDF、Probability 和 RandomFunction 一起使用.
范例
打开所有单元 关闭所有单元范围 (10)
过程切片性质 (5)
应用 (3)
属性和关系 (3)
InhomogeneousPoissonProcess 是一个跳跃过程:
带有常密度的非齐次泊松过程是 PoissonProcess:
文本
Wolfram Research (2015),InhomogeneousPoissonProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html.
CMS
Wolfram 语言. 2015. "InhomogeneousPoissonProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html.
APA
Wolfram 语言. (2015). InhomogeneousPoissonProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html 年
BibTeX
@misc{reference.wolfram_2025_inhomogeneouspoissonprocess, author="Wolfram Research", title="{InhomogeneousPoissonProcess}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_inhomogeneouspoissonprocess, organization={Wolfram Research}, title={InhomogeneousPoissonProcess}, year={2015}, url={https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html}, note=[Accessed: 07-February-2026]}