InverseErf

InverseErf[s]

给出作为 z 在 的解的逆误差函数.

更多信息

  • 数学函数，适宜于符号和数值运算.
  • 仅在 s 的实数值在 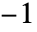和 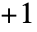之间时，给出明确的数值.
  • InverseErf[z0,s] 给出广义误差函数 Erf[z0,z] 的逆函数.
  • 对于某些特定参数，InverseErf 自动运算出精确值.
  • InverseErf 可求任意数值精度的值.
  • InverseErf 可与 Interval 和 CenteredInterval 对象一起使用. »
  • InverseErf 自动逐项作用于列表的各个元素.

范例

打开所有单元关闭所有单元

基本范例  (4)

数值运算：

在实数的子集上绘图：

原点处的级数展开式：

奇点处的级数展开式：

范围  (32)

数值计算  (5)

高精度数值运算：

输出精度与输入精度一致：

在高精度条件下高效计算 InverseErf：

计算广义误差函数的逆函数的值：

用 Interval 和 CenteredInterval 对象计算最坏情况下的区间：

或用 Around 计算一般情况下的统计区间：

计算数组中每个元素的值：

或用 MatrixFunction 计算矩阵形式的 InverseErf 函数：

特殊值  (2)

参数取特定值时的精确结果：

求方程 的实根：

可视化  (3)

绘制 InverseErf 函数：

绘制 取不同值时广义误差函数的逆函数：

绘制 取不同值时广义误差函数的逆函数：

函数的属性  (9)

InverseErf 对区间 () 内的所有实数值有定义：

InverseErf 的值域是所有实数：

InverseErf 是奇函数：

InverseErf 在定义域上是解析函数：

一般情况下，它不是解析函数，因为它既有奇点，也有断点：

InverseErf 在定义域上非递减：

InverseErf 是单射函数：

InverseErf 是满射函数：

InverseErf 既不是非负，也不是非正：

InverseErf 在定义域上既不凸，也不凹：

微分  (2)

一阶导数：

高阶导数：

积分  (3)

InverseErf 的不定积分：

实定义域上 InverseErf 的定积分：

InverseErf 定积分的数值近似：

级数展开  (2)

InverseErf 的泰勒展开式：

绘制 附近 InverseErf 的前 3 个近似式：

广义误差函数的逆函数的级数展开式：

函数恒等式和化简  (2)

与逆误差函数一起使用：

与逆广义误差函数一起使用：

函数表示  (4)

逆误差函数的主定义：

与广义误差函数的逆函数的关系：

与逆互补误差函数的关系：

TraditionalForm 格式：

应用  (3)

产生高斯分布的随机数：

在高斯分布中，高斯分布中 99% 置信区间的标准差的数量：

绘制 InverseErf：

属性和关系  (5)

求解一个超越方程：

求超越方程的数值根：

获取作为一个微分方程的解的 InverseErf：

InverseErf 是一个数值函数：

在 TraditionalForm 中， 被自动解释为逆误差函数：

可能存在的问题  (1)

InverseErf 仅在 时进行数值计算：

巧妙范例  (1)

InverseErf 的黎曼曲面：

Wolfram Research (1996)，InverseErf，Wolfram 语言函数，https://reference.wolfram.com/language/ref/InverseErf.html （更新于 2023 年）.

文本

Wolfram Research (1996)，InverseErf，Wolfram 语言函数，https://reference.wolfram.com/language/ref/InverseErf.html （更新于 2023 年）.

CMS

Wolfram 语言. 1996. "InverseErf." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2023. https://reference.wolfram.com/language/ref/InverseErf.html.

APA

Wolfram 语言. (1996). InverseErf. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/InverseErf.html 年

BibTeX

@misc{reference.wolfram_2024_inverseerf, author="Wolfram Research", title="{InverseErf}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/InverseErf.html}", note=[Accessed: 25-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inverseerf, organization={Wolfram Research}, title={InverseErf}, year={2023}, url={https://reference.wolfram.com/language/ref/InverseErf.html}, note=[Accessed: 25-November-2024 ]}