WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

InverseSurvivalFunction[dist,q]

分布 dist の生存関数の逆関数を変数 q の関数として与える．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
パラメトリック分布  
派生分布  
ノンパラメトリック分布  
ランダム過程  
一般化と拡張  
アプリケーション  
特性と関係  
考えられる問題  
関連項目
関連するガイド
履歴
引用書式

InverseSurvivalFunction

InverseSurvivalFunction[dist,q]

分布 dist の生存関数の逆関数を変数 q の関数として与える．

詳細

  • q における逆生存関数は分布の第(1-q)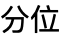分位に等しい．
  • 連続分布 dist について，q における逆生存関数はSurvivalFunction[dist,x]q となる値 x である．
  • 離散分布 dist について，q における逆生存関数はSurvivalFunction[dist,x]≤q となる最小の整数 x である．
  • 値 q は記号でもよく，0から1までの任意の数でもよい．

例題

すべて開く すべて閉じる

例  (2)

一変量連続分布の逆生存関数：

Wolfram Language code: Plot[Table[InverseSurvivalFunction[BetaDistribution[1 / 2, β], q], {β, {1 / 4, 1 / 2, 1}}]//Evaluate, {q, 0, 1}, Filling -> Axis]
Wolfram Language code: InverseSurvivalFunction[BetaDistribution[α, β], q]

一変量離散分布の逆生存関数：

Wolfram Language code: 𝒟 = PoissonDistribution[5];
Wolfram Language code: DiscretePlot[InverseSurvivalFunction[𝒟, p], {p, SurvivalFunction[𝒟, Range[0, 10]]}, ExtentSize -> Right, ExtentMarkers -> {"Empty", "Filled"}]

スコープ  (11)

パラメトリック分布  (4)

厳密な数値結果を得る：

Wolfram Language code: InverseSurvivalFunction[ExponentialDistribution[2], 1 / 4]
Wolfram Language code: InverseSurvivalFunction[NegativeBinomialDistribution[20, 1 / 3], 1 / 5]

機械精度の結果を得る：

Wolfram Language code: InverseSurvivalFunction[WeibullDistribution[2, 5], 0.4]

連続分布について任意精度の結果を得る：

Wolfram Language code: InverseSurvivalFunction[WeibullDistribution[2, 5], N[1 / 14, 25]]

逆生存関数の記号式を得る：

Wolfram Language code: InverseSurvivalFunction[ChiSquareDistribution[ν], x]

派生分布  (3)

指数分布の二次変換：

Wolfram Language code: InverseSurvivalFunction[TransformedDistribution[x ^ 2, xExponentialDistribution[2]], y]
Wolfram Language code: Plot[%, {y, 0, 1}, Filling -> Axis]

切断分布：

Wolfram Language code: isf = InverseSurvivalFunction[TruncatedDistribution[{2, 3}, TriangularDistribution[{1, 4}]], x]
Wolfram Language code: Plot[isf, {x, 0, 1}, Filling -> Axis, Exclusions -> None]

単位付き数量を含む分布についてのInverseSurvivalFunction：

Wolfram Language code: InverseSurvivalFunction[MaxwellDistribution[Quantity[45.3, "Meters"/"Seconds"]], Quantity[96, "Percent"]]

データ分布について：

Wolfram Language code: sample = QuantityArray[RandomVariate[NormalDistribution[2, 5], 1000], "Grams"]
Wolfram Language code: InverseSurvivalFunction[SmoothKernelDistribution[sample], 0.7]

ノンパラメトリック分布  (2)

ノンパラメトリック分布の逆生存関数：

Wolfram Language code: r = RandomVariate[NormalDistribution[], 10 ^ 3];
Wolfram Language code: InverseSurvivalFunction[HistogramDistribution[r], 0.2]
Wolfram Language code: InverseSurvivalFunction[SmoothKernelDistribution[r], 0.2]
Wolfram Language code: InverseSurvivalFunction[KernelMixtureDistribution[r], 0.2]
Wolfram Language code: InverseSurvivalFunction[SurvivalDistribution[r], 0.2]
Wolfram Language code: InverseSurvivalFunction[EmpiricalDistribution[r], 0.2]

もとになっているパラメトリック分布の値と比較する：

Wolfram Language code: InverseSurvivalFunction[NormalDistribution[], 0.2]

ヒストグラム分布の生存関数をプロットする：

Wolfram Language code: Plot[InverseSurvivalFunction[HistogramDistribution[RandomVariate[NormalDistribution[], 10 ^ 3]], x]//Evaluate, {x, 0, 1}, Filling -> Axis, Exclusions -> None]

ランダム過程  (2)

ランダム過程のSliceDistributionについてのInverseSurvivalFunction：

Wolfram Language code: InverseSurvivalFunction[WienerProcess[μ, σ][t], q]
Wolfram Language code: Plot[Evaluate[% /. {μ -> 3, σ -> 1, q -> 1 / 20}], {t, 0, 1}]

ある時点 t=0.5におけるTemporalDataのInverseSurvivalFunctionを求める：

Wolfram Language code: td = RandomFunction[WienerProcess[1, 1], {0, 10, 0.05}, 100]
Wolfram Language code: InverseSurvivalFunction[td[0.5], 0.4]

ある時間範囲についてのInverseSurvivalFunctionをすべてのシミュレーションとともに求める：

Wolfram Language code: Show[ListLinePlot[td, PlotStyle -> Directive[Opacity[0.2], Thin]], Plot[InverseSurvivalFunction[td[t], 0.4], {t, 0, 10}, PlotStyle -> Thick]]

一般化と拡張  (1)

InverseSurvivalFunctionは要素単位でリストに縫い込まれる：

Wolfram Language code: InverseSurvivalFunction[NormalDistribution[], {0.2, 0.3}]
Wolfram Language code: {InverseSurvivalFunction[NormalDistribution[], 0.2], InverseSurvivalFunction[NormalDistribution[], 0.3]}

アプリケーション  (3)

標準正規分布の逆生存関数をプロットする：

Wolfram Language code: Plot[InverseSurvivalFunction[NormalDistribution[0, 1], q], {q, 0, 1}]

二項分布の逆生存関数をプロットする：

Wolfram Language code: Plot[InverseSurvivalFunction[BinomialDistribution[20, .5], q], {q, 0, 1}, PlotRange -> {0, 20}]

分布から乱数を生成する：

Wolfram Language code: InverseSurvivalFunction[StudentTDistribution[20], RandomReal[]]

特性と関係  (3)

InverseSurvivalFunctionとSurvivalFunctionは，連続分布については逆関数である：

Wolfram Language code: dist = ExponentialDistribution[λ];
Wolfram Language code: Assuming[y > 0 && λ > 0, Simplify[InverseSurvivalFunction[dist, SurvivalFunction[dist, y]] == y]]
Wolfram Language code: Assuming[1 > q > 0 && λ > 0, Simplify[SurvivalFunction[dist, InverseSurvivalFunction[dist, q]] == q]]

InverseSurvivalFunctionとSurvivalFunctionの合成は離散分布のステップ関数を与える：

Wolfram Language code: dist = PoissonDistribution[2];
Wolfram Language code: Plot[SurvivalFunction[dist, InverseSurvivalFunction[dist, q]], {q, 0, 1}, Exclusions -> None]
Wolfram Language code: Plot[InverseSurvivalFunction[dist, SurvivalFunction[dist, y]], {y, 0, 10}, Exclusions -> None]

InverseSurvivalFunctionは分布に関してはInverseCDFに等しい：

Wolfram Language code: InverseSurvivalFunction [CauchyDistribution[a, b], q]
Wolfram Language code: InverseCDF[CauchyDistribution[a, b], 1 - q]
Wolfram Language code: Simplify[% - %%, 0 < q < 1]

考えられる問題  (2)

記号閉形式が存在しない分布もある：

Wolfram Language code: InverseSurvivalFunction[BinomialDistribution[50, .5], q]

数値評価は可能である：

Wolfram Language code: InverseSurvivalFunction[BinomialDistribution[50, .5], .75]

入力を引数として与える場合は完全な検証が行われ無効な入力は評価されない：

Wolfram Language code: InverseSurvivalFunction[CauchyDistribution[2, 3], 1. + I]
Wolfram Research (2010), InverseSurvivalFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseSurvivalFunction.html.

テキスト

Wolfram Research (2010), InverseSurvivalFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseSurvivalFunction.html.

CMS

Wolfram Language. 2010. "InverseSurvivalFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseSurvivalFunction.html.

APA

Wolfram Language. (2010). InverseSurvivalFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseSurvivalFunction.html

BibTeX

@misc{reference.wolfram_2026_inversesurvivalfunction, author="Wolfram Research", title="{InverseSurvivalFunction}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/InverseSurvivalFunction.html}", note=[Accessed: 02-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_inversesurvivalfunction, organization={Wolfram Research}, title={InverseSurvivalFunction}, year={2010}, url={https://reference.wolfram.com/language/ref/InverseSurvivalFunction.html}, note=[Accessed: 02-November-2026]}