Quantile

Quantile[data,p]

gives the estimate of the p^(th) quantile of data.

Quantile[data,{p1,p2,…}]

gives a list of quantiles p1,p2,….

Quantile[data,p,{{a,b},{c,d}}]

uses the quantile definition specified by parameters a, b, c, d.

Quantile[dist,p]

gives a quantile of the distribution dist.

Details

  • Quantile is also known as value at risk (VaR) or fractile.
  • When VectorQ data 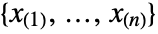is sorted as 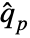, the quantile estimate 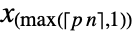is given by .
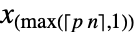  • For MatrixQ data, the quantile is computed for each column vector with Quantile[{{x1,y1,…},{x2,y2,…},…},p] equivalent to {Quantile[{x1,x2,…},p],Quantile[{y1,y2,…},p]}. »
  • For ArrayQ data, quantile is equivalent to ArrayReduce[Quantile,data,1]. »
  • Quantile[{x_1,...,x_n},p,{{a,b},{c,d}}] is given by 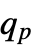with r=a+(n+b)p, ⌊r⌋= Floor[r], ⌈r⌉=Ceiling[r] and =FractionalPart[r]. The indices are taken to be 1 or n if they are out of range. »
  • Common choices of parameters {{a,b},{c,d}} include:
  • {{0,0},{1,0}}inverse empirical CDF (default)
    {{0,0},{0,1}}linear interpolation (California method)
    {{1/2,0},{0,0}}element numbered closest to p n
    {{1/2,0},{0,1}}linear interpolation (hydrologist method)
    {{0,1},{0,1}}mean‐based estimate (Weibull method)
    {{1,-1},{0,1}}mode‐based estimate
    {{1/3,1/3},{0,1}}median‐based estimate
    {{3/8,1/4},{0,1}}normal distribution estimate
  • The default choice of parameters is {{0,0},{1,0}}.
  • About 10 different choices of parameters are in use in statistical work.
  • Quantile[list,p] always gives a result equal to an element of list.
  • The same is true whenever d is 0.
  • When d is 1, Quantile is piecewise linear as a function of p.
  • Median[data] is equivalent to Quantile[data,1/2,{{1/2,0},{0,1}}].
  • The data can have the following additional forms and interpretations:
  • Associationthe values (the keys are ignored) »
    SparseArrayas an array, equivalent to Normal[data] »
    QuantityArrayquantities as an array »
    WeightedDatabased on the underlying EmpiricalDistribution »
    EventDatabased on the underlying SurvivalDistribution »
    TimeSeries, TemporalData, …vector or array of values (the time stamps ignored) »
    Image,Image3DRGB channel's values or grayscale intensity value »
    Audioamplitude values of all channels »
    DateObject, TimeObjectlist of dates or list of times »
  • Quantile[dist,p] is equivalent to InverseCDF[dist,p].
  • Quantile[dist,p] is the minimum of the set of number(s) 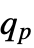q_(p) such that Probability[x≤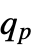q_(p),xdist]≥p and Probability[x≥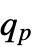q_(p),xdist]≥p. »
  • For a random process proc, the quantile function can be computed for slice distribution at time t, SliceDistribution[proc,t], as Quantile[SliceDistribution[proc,t], p]. »
  • The value p can be symbolic or any number between 0 and 1. »

Examples

open allclose all

Basic Examples  (7)

Find the halfway value of a list:

Find the 20% and 80% quantiles of a list:

Find the top percentile of a list:

Quantile of a list of dates:

The q^(th) quantile for a normal distribution:

Quantile function for a continuous univariate distribution:

Quantile function for a discrete univariate distribution:

Scope  (33)

Basic Uses  (7)

Quantile works with any real numeric quantities:

Obtain results at any precision:

Compute results using other parametrizations:

Find quantiles for WeightedData:

Find quantiles for EventData:

Find a quantile for TimeSeries:

The quantile depends only on the values:

Find a quantile for data involving quantities:

Array Data  (6)

Find quantiles of elements in each column:

Find multiple quantiles of elements in each column:

The quantile for a tensor gives columnwise standard deviations at the first level:

Compute results for a large vector or matrix:

When the input is an Association, Quantile works on its values:

Compute results for a SparseArray:

Find a quantile of a QuantityArray:

Image and Audio Data  (2)

Channelwise 30% percentile value of an RGB image:

30% percentile intensity value of a grayscale image:

30% percentile amplitude of all channels:

Date and Time  (5)

Compute a quantile of dates:

Compute a weighted quantile of dates:

Compute a quantile of dates given in different calendars:

The quantile is given in one of the input calendars:

Compute a quantile of times:

Compute a quantile of times with different time zone specifications:

Parametric Distributions  (5)

Obtain exact numeric results:

Obtain a machine-precision result:

Obtain a result at any precision for a continuous distribution:

Obtain a symbolic expression for the quantile:

Quantile threads elementwise over lists:

Nonparametric Distributions  (2)

Quantile for nonparametric distributions:

Compare with the value for the underlying parametric distribution:

Plot the quantile for a histogram distribution:

Derived Distributions  (4)

Quantile for a truncated distribution:

Quadratic transformation of an exponential distribution:

Censored distribution:

Quantile for distributions with quantities:

Random Processes  (2)

Quantile function for a random process:

Find a quantile of TemporalData at some time t=0.5:

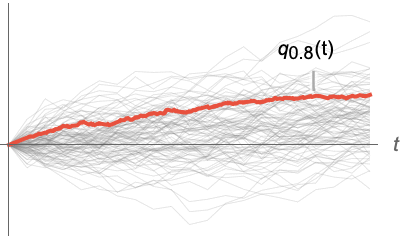
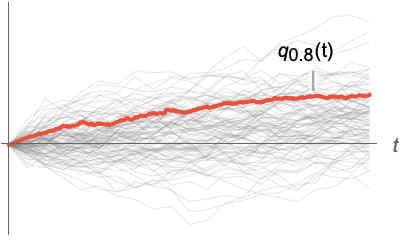
Find the corresponding quantile function together with all the simulations:

Applications  (7)

A set of equally spaced quantiles divides the values into equal-sized groups:

Calculate a set of quantiles:

Plot the PDF divided according to the values of quantiles into five regions:

Use quantile as a mesh function:

Plot the q^(th) quantile for a list:

The linearly interpolated quantile:

Compute an expectation using quantile :

Use this method in Expectation:

Generate random numbers for a nonuniform distribution by transforming the uniform distribution by the quantile function of the nonuniform distribution:

Compare the histogram of the sample with the probability density function of the desired distribution:

Compute a moving quantile for some data:

Use the window of length .1:

Compute selected quantiles for slices of a collection of paths of a random process:

Choose a few slice times:

Plot the quantiles over these paths:

Compute quantiles for the heights of children in a class:

Properties & Relations  (9)

Use Quantile to find the quartiles of a distribution:

Calculate quartiles directly:

With default parameters, Quantile always returns an element of the list:

Quartiles gives linearly interpolated Quantile values for a list:

InterquartileRange is the difference of linearly interpolated Quantile values for a list:

QuartileDeviation is half the difference of linearly interpolated Quantile values for a list:

QuartileSkewness uses linearly interpolated Quantile values as a skewness measure:

Quantile is equivalent to InverseCDF for distributions:

QuantilePlot plots the quantiles of a list or distribution:

BoxWhiskerChart shows special quantiles for data:

Possible Issues  (4)

For computations with data, the value p can be any number between 0 and 1:

The symbolic closed form may exist for some distributions:

Symbolic closed forms do not exist for some distributions:

Numerical evaluation works:

Substitution of invalid values into symbolic outputs gives results that are not meaningful:

It stays unevaluated if passed as an argument:

Quartiles of data computed via Quantile do not always agree with Quartiles:

Calculate quartiles directly:

Specify linear interpolation parameters in Quantile:

Neat Examples  (1)

The distribution of Quantile estimates for 20, 100, and 300 samples:

Wolfram Research (2003), Quantile, Wolfram Language function, https://reference.wolfram.com/language/ref/Quantile.html (updated 2024).

Text

Wolfram Research (2003), Quantile, Wolfram Language function, https://reference.wolfram.com/language/ref/Quantile.html (updated 2024).

CMS

Wolfram Language. 2003. "Quantile." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Quantile.html.

APA

Wolfram Language. (2003). Quantile. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Quantile.html

BibTeX

@misc{reference.wolfram_2025_quantile, author="Wolfram Research", title="{Quantile}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Quantile.html}", note=[Accessed: 22-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_quantile, organization={Wolfram Research}, title={Quantile}, year={2024}, url={https://reference.wolfram.com/language/ref/Quantile.html}, note=[Accessed: 22-February-2025 ]}