KaiserWindow

KaiserWindow[x]

x のカイザー(Kaiser)窓関数を表す．

KaiserWindow[x,α]

パラメータ α を使う．

詳細

  • KaiserWindowは，Kaiser–Bessel窓としても知られているもので，一般に有限インパルス応答(FIR)フィルタ設計とスペクトル分析に使用される窓関数である．
  • 窓関数は，データが短いセグメントで処理されるアプリケーションに使われ，データ値を漸減して各セグメントの終りで0に近付ける平滑化効果がある．
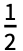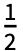  • KaiserWindow[x,α]は，-≤x≤のときはに等しくそれ以外では0である．
  • KaiserWindow[x]はKaiserWindow[x,3]と等価である．
  • KaiserWindowは自動的にリストに縫い込まれる．

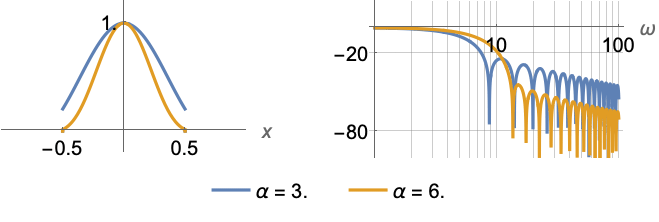
例題

すべて開くすべて閉じる

例  (3)

1Dカイザー窓の形：

2Dカイザー窓の形：

カイザー窓を表す連続関数を抽出する：

パラメータ化されたカイザー窓：

スコープ  (8)

数値的に評価する：

指定のパラメータを使った1Dカイザー窓の形：

平行移動され拡張されたカイザー窓：

パラメータ α の関数としての形の変化：

2Dカイザー窓の形状：

円形の台を持つ二次元カイザー窓：

長さ15の離散カイザー窓：

15×10の離散二次元カイザー窓：

アプリケーション  (5)

カイザー窓を使ってスペクトログラムを計算する際の信号分割の影響を減らす：

カットオフ周波数 ，長さ15のローパス有限インパルス応答フィルタを作る：

このフィルタにカイザー窓を適用してストップバンド元帥を向上させる：

2つのフィルタのパワースペクトルの対数振幅プロット：

カイザー窓メソッドを使ってホワイトノイズ信号にフィルタをかける：

窓指定を使ってARMA過程のサンプルPowerSpectralDensityを計算する：

スペクトルを計算する：

窓関数を使わずに計算されたスペクトル密度と比較する：

プロットは，窓がスペクトル密度を平坦化したことを示している：

この過程の理論的なスペクトル密度と比較する：

時系列推定に窓指定を使う：

スペクトル推定器に窓を指定する：

特性と関係  (8)

カイザー窓の下の面積：

正規化することで単位面積の窓を作る：

カイザー窓のフーリエ変換：

カイザー窓のパワースペクトル：

パラメータ化されたカイザー窓のフーリエ変換：

パラメータ α の関数としての振幅スペクトルのバリエーション：

長さ15の離散カイザー窓：

係数の合計が1になるように正規化する：

正規化された長さ15の離散カイザー窓の離散時間フーリエ変換：

振幅スペクトル：

デフォルトのカイザー窓と矩形窓のパワースペクトル：

異なる3つの窓の長さについてのパワースペクトル：

形状パラメータ α の異なる3つの値についてのパワースペクトル：

考えられる問題  (1)

Arrayに記号として渡す場合には，カイザー窓の2Dサンプリングはサンプルの各行に異なるパタメータを用いる：

代りに純関数を使う：

Wolfram Research (2012), KaiserWindow, Wolfram言語関数， https://reference.wolfram.com/language/ref/KaiserWindow.html.

テキスト

Wolfram Research (2012), KaiserWindow, Wolfram言語関数， https://reference.wolfram.com/language/ref/KaiserWindow.html.

CMS

Wolfram Language. 2012. "KaiserWindow." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/KaiserWindow.html.

APA

Wolfram Language. (2012). KaiserWindow. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KaiserWindow.html

BibTeX

@misc{reference.wolfram_2024_kaiserwindow, author="Wolfram Research", title="{KaiserWindow}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/KaiserWindow.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_kaiserwindow, organization={Wolfram Research}, title={KaiserWindow}, year={2012}, url={https://reference.wolfram.com/language/ref/KaiserWindow.html}, note=[Accessed: 18-November-2024 ]}