KaiserWindow

KaiserWindow[x]

表示关于 x 的 Kaiser 窗函数.

KaiserWindow[x,α]

使用参数 α.

更多信息

  • KaiserWindow，亦称为 Kaiser–Bessel 窗，是一个窗函数，通常用于设计有限冲激响应滤波器 (FIR) 和频谱分析.
  • 窗函数被用在以较短的片段来处理数据的应用中，并且通过在每个片段的末尾将数据值逐渐减小为零来产生平滑效果.
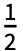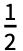  • 对于 -≤x≤，KaiserWindow[x,α] 等价于 ，否则为零.
  • KaiserWindow[x] 等价于 KaiserWindow[x,3].
  • KaiserWindow 自动线性作用于列表.

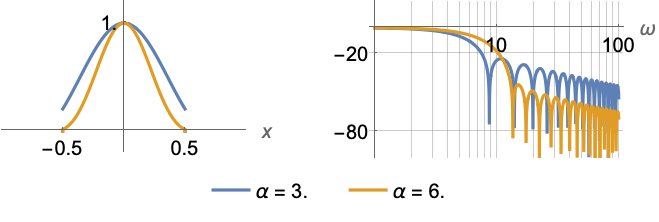
范例

打开所有单元关闭所有单元

基本范例  (3)

一维 Kaiser 窗的形状：

二维 Kaiser 窗的形状：

提取表示 Kaiser 窗的连续函数：

参数化 Kaiser 窗：

范围  (8)

数值运算：

使用指定的参数表示一维 Kaiser 窗的形状：

Kaiser 窗的变换和伸缩：

以参数 α 的函数表示的形状变化：

圆形边缘的二维 Kaiser 窗：

具有圆形支撑的二维 Kaiser 窗函数：

长度为 15 的离散 Kaiser 窗：

离散15×10 二维 Kaiser 窗：

应用  (5)

计算频谱图时，使用 Kaiser 窗函数来减小分割信号所造成的影响：

创建一个截止频率为 、长度为 15 的低通 FIR 滤波器：

对滤波器应用 Kaiser 窗，改善阻带衰减：

两个滤波器的功率谱的对数幅度图：

使用 Kaiser 窗对白噪声信号进行滤波：

使用窗口规范计算 ARMA 过程的 PowerSpectralDensity 样本：

计算光谱：

与没有窗函数计算的光谱密度比较：

下图显示窗函数对光谱密度进行平滑处理：

与过程的理论光谱密度比较：

使用时间序列估计的窗指定：

指定光谱估计器的窗函数：

属性和关系  (8)

Kaiser 窗下的面积：

规范化以创建单位面积的窗：

Kaiser 窗的傅立叶变换：

Kaiser 窗的功率谱：

参数化 Kaiser 窗的傅立叶变换：

幅度谱随参数 α 的变化：

长度为 15 的离散 Kaiser 窗函数：

归一化，使系数相加为 1：

长度为 15 的归一化离散 Kaiser 窗函数的离散时间傅立叶变换：

幅值谱：

默认的 Kaiser 窗函数和矩形窗函数的功率谱：

三种不同窗口长度情形下的功率谱：

形状参数 α 取三个不同值时的功率谱：

可能存在的问题  (1)

当作为符号传递给 Array 时，Kaiser 窗口的二维采样将对每行样本使用不同的参数：

使用纯函数：

Wolfram Research (2012)，KaiserWindow，Wolfram 语言函数，https://reference.wolfram.com/language/ref/KaiserWindow.html.

文本

Wolfram Research (2012)，KaiserWindow，Wolfram 语言函数，https://reference.wolfram.com/language/ref/KaiserWindow.html.

CMS

Wolfram 语言. 2012. "KaiserWindow." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/KaiserWindow.html.

APA

Wolfram 语言. (2012). KaiserWindow. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/KaiserWindow.html 年

BibTeX

@misc{reference.wolfram_2024_kaiserwindow, author="Wolfram Research", title="{KaiserWindow}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/KaiserWindow.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_kaiserwindow, organization={Wolfram Research}, title={KaiserWindow}, year={2012}, url={https://reference.wolfram.com/language/ref/KaiserWindow.html}, note=[Accessed: 18-November-2024 ]}