LearningRateMultipliers

LearningRateMultipliers

is an option for net layers and for NetTrain, NetChain, NetGraph that specifies learning rate multipliers to apply during training.

Details

  • With the default value of LearningRateMultipliers->Automatic, all layers learn at the same rate.
  • LearningRateMultipliers->{rule1,rule2,…} specifies a set of rules that will be used to determine learning rate multipliers for every trainable array in the net.
  • In LearningRateMultipliers->{rule1,rule2,…}, each of the rulei can be of the following forms:
  • "part"ruse multiplier r for a named layer, subnetwork or array in a layer
    nruse multiplier r for the n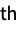^(th) layer
    m;;nruse multiplier r for layers m through n
    {part1,part2,…}ruse multiplier r for a nested layer or array
    _ruse multiplier r for all layers
  • LearningRateMultipliersr specifies using the same multiplier r for all trainable arrays.
  • If r is zero or None, it specifies that the layer or array should not undergo training and will be left unchanged by NetTrain.
  • If r is a positive or negative number, it specifies a multiplier to apply to the global learning rate chosen by the training method to determine the learning rate for the given layer or array.
  • For each trainable array, the rate used is given by the first matching rule, or 1 if no rule matches.
  • Rules that specify a subnet (e.g. a nested NetChain or NetGraph) apply to all layers and arrays within that subnet.
  • LearningRateMultipliers->{part->None} can be used to "freeze" a specific part.
  • LearningRateMultipliers->{part->1,_->None} can be used to "freeze" all layers except for a specific part.
  • The hierarchical specification {part1,part2,…} used by LearningRateMultipliers to refer to parts of a net is equivalent to that used by NetExtract and NetReplacePart.
  • Information[net,"ArraysLearningRateMultipliers"] yields the default learning rate multipliers for all arrays of a net.
  • The multipliers that are genuinely used when training can be obtained from a NetTrainResultsObject via the property "ArraysLearningRateMultipliers".

Examples

open allclose all

Basic Examples  (2)

Create and initialize a net with three layers, but train only the last layer:

Evaluate the trained net on an input:

The first layer of the initial net started with zero biases:

The biases of the first layer remain zero in the trained net:

The biases of the third layer have been trained:

Create a frozen layer with given array values:

Nest this layer inside a bigger net:

Get the learning rate multipliers that will be used by default in NetTrain, for all arrays of the net:

Train with the net:

Check the learning rate multipliers that were used to train:

The arrays of the frozen layer were unchanged during training:

Scope  (1)

Replace LearningRateMultipliers in a Network  (1)

Take a net:

Set the LearningRateMultipliers of the first layer of this net to zero:

Check programmatically the values of LearningRateMultipliers options:

Applications  (1)

Train an existing network to solve a new task. Obtain a pre-trained convolutional model that was trained on handwritten digits:

Remove the final two layers, and attach two new layers, in order to classify images into 3 classes:

Generate training data by rasterizing the characters "x", "y", and "z" with a variety of fonts, sizes, and cases:

Train the modified network on the new task:

Classify an unseen letter:

Measure the performance on the original training data, which includes the training and validation set:

Properties & Relations  (1)

Train LeNet on the MNIST dataset with specific learning rate multipliers, returning a NetTrainResultsObject:

Obtain the actual learning rate multipliers used on individual weight arrays:

Possible Issues  (1)

When a shared array occurs at several places in the network, only a unique learning rate multiplier will be applied to all the occurrences of the shared array.

Create a network with shared arrays:

Specifying a LearningRateMultipliers to a shared array in the network will assign the same multiplier to all places:

If there is a conflict, the first matching value will be used:

The same happens when LearningRateMultipliers is specified when constructing the network:

Wolfram Research (2017), LearningRateMultipliers, Wolfram Language function, https://reference.wolfram.com/language/ref/LearningRateMultipliers.html (updated 2020).

Text

Wolfram Research (2017), LearningRateMultipliers, Wolfram Language function, https://reference.wolfram.com/language/ref/LearningRateMultipliers.html (updated 2020).

CMS

Wolfram Language. 2017. "LearningRateMultipliers." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/LearningRateMultipliers.html.

APA

Wolfram Language. (2017). LearningRateMultipliers. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LearningRateMultipliers.html

BibTeX

@misc{reference.wolfram_2025_learningratemultipliers, author="Wolfram Research", title="{LearningRateMultipliers}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/LearningRateMultipliers.html}", note=[Accessed: 30-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_learningratemultipliers, organization={Wolfram Research}, title={LearningRateMultipliers}, year={2020}, url={https://reference.wolfram.com/language/ref/LearningRateMultipliers.html}, note=[Accessed: 30-June-2025 ]}