LegendreQ
詳細

- 記号操作・数値操作の両方に適した数学関数である.
- 整数 n と m について,明示的な式が作成される.
- ルジャンドル関数は微分方程式
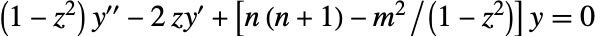 を満たす.
を満たす. - LegendreQ[n,m,a,z]は,タイプ a のルジャンドル関数を与える.デフォルトのタイプは1である.
- タイプ1,2,3のLegendreQは,これらのタイプのLegendrePによって定義され,LegendrePで説明されているのと同じ分枝切断線構造と特性を持つ.
- 特別な引数の場合,LegendreQは,自動的に厳密値を計算する.
- LegendreQは任意の数値精度で評価できる.
- LegendreQは自動的にリストに縫い込まれる.
- LegendreQはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
例題
すべて開くすべて閉じる例 (6)
スコープ (42)
数値評価 (6)
LegendreQを高精度で効率よく評価する:
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する:
Aroundを使って平均的な場合の統計区間を計算することもできる:
MatrixFunctionを使って行列のLegendreQ関数を計算することもできる:
特定の値 (5)
可視化 (3)
関数の特性 (12)
級数展開 (4)
関数の恒等式と簡約 (2)
関数表現 (4)
LegendreQはDifferentialRootとして表すことができる:
TraditionalFormによる表示:
一般化と拡張 (2)
アプリケーション (4)
Pöschl–Tellerポテンシャルは1次元のシュレディンガー(Schrödinger)方程式を特殊関数で解くことができる特別なクラスのポテンシャルである.
修正Pöschl–Tellerポテンシャルの量子固有関数を求める:
n 点ガウス求積法は n 次のルジャンドル多項式に基づいている.n 点ガウス求積法のノードと重みを計算する:
ガウス求積法をクロンロッド(Kronrod)が拡張したものは,n+1 点を加えてガウス求積の n ノードを再利用し,結果として2n+1点の積分法になる.追加の n+1ノードは第2種ルジャンドル関数(スティルチェス(Stieltjes)多項式)の漸近展開から構築された多項式の根として取得できる:
(2n+1)点のガウス・クロンロッド法を使って積分を数値評価する:
ガウス・クロンロッド法とガウス法の違いは誤差推定に使うことができる:
ガウス・クロンロッド法の結果をNIntegrateの結果と比較する:
特性と関係 (2)
テキスト
Wolfram Research (1988), LegendreQ, Wolfram言語関数, https://reference.wolfram.com/language/ref/LegendreQ.html (2022年に更新).
CMS
Wolfram Language. 1988. "LegendreQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/LegendreQ.html.
APA
Wolfram Language. (1988). LegendreQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LegendreQ.html