is an option for GeneralizedLinearModelFit that specifies the link function for the generalized linear model.


LinkFunction
is an option for GeneralizedLinearModelFit that specifies the link function for the generalized linear model.
Details


- The link function is an invertible function
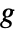 in the generalized linear model
in the generalized linear model 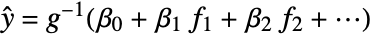 .
. - Possible settings for LinkFunction include:
-
Automatic automatically determined "name" named link function g invertible function - The default value Automatic uses the canonical link for the ExponentialFamily associated with the model.
- The canonical link functions are as follows:
-
"LogitLink" 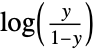
used for "Binomial" "ReciprocalLink" 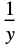
used for "Gamma" "IdentityLink" 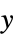
used for "Gaussian" "InverseSquareLink" 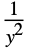
used for "InverseGaussian" "LogLink" 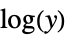
used for "Poisson" - For "QuasiLikelihood" models, "IdentityLink" is used by default.
- Other common link functions for binomial data include:
-
"ProbitLink" 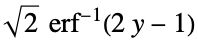
"CauchitLink" 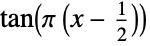
"LogLogLink" 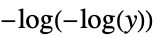
"LogComplementLink" 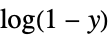
"ComplementaryLogLogLink" 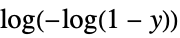
"OddsPowerLink" 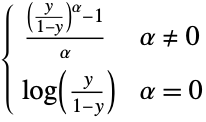
- Other common link functions for count data include:
-
"NegativeBinomialLink" 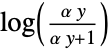
- Other common link functions for positive real‐valued data include:
-
"PowerLink" 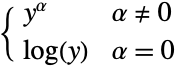
- For "OddsPowerLink", "NegativeBinomialLink", and "PowerLink", the additional parameter α can be given by LinkFunction->{linkname,"LinkParameter"->α}. The parameter α can be any real value for "OddsPowerLink" and "PowerLink" and any positive value for "NegativeBinomialLink".
- With setting LinkFunction->g, g can be any pure function that is real‐valued and invertible on the response domain for the model.
Related Guides
History
Text
Wolfram Research (2008), LinkFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/LinkFunction.html.
CMS
Wolfram Language. 2008. "LinkFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LinkFunction.html.
APA
Wolfram Language. (2008). LinkFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LinkFunction.html
BibTeX
@misc{reference.wolfram_2025_linkfunction, author="Wolfram Research", title="{LinkFunction}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/LinkFunction.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_linkfunction, organization={Wolfram Research}, title={LinkFunction}, year={2008}, url={https://reference.wolfram.com/language/ref/LinkFunction.html}, note=[Accessed: 25-February-2026]}