LinkFunction

LinkFunction

GeneralizedLinearModelFitのオプションで，一般化された線形モデルのリンク関数を指定する．

詳細

  • リンク関数は一般化された線形モデル 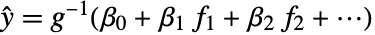中の可逆関数 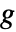である．
  • LinkFunctionの可能な設定値
  • Automatic自動的に決定される
    "name"名前付きリンク関数
    g可逆関数
  • デフォルト値のAutomaticはモデルと関連したExponentialFamilyに正準リンクを使う．
  • 正凖リンク関数は次の通りである．
  • "LogitLink"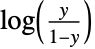"Binomial"に使われる
    "ReciprocalLink"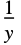"Gamma"に使われる
    "IdentityLink"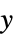"Gaussian"に使われる
    "InverseSquareLink"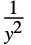"InverseGaussian"に使われる
    "LogLink"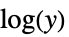"Poisson"に使われる
  • "QuasiLikelihood"モデルについては"IdentityLink"がデフォルトで使われる．
  • 二項データの上記以外の一般的なリンク関数
  • "ProbitLink"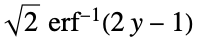
    "CauchitLink"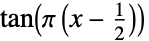
    "LogLogLink"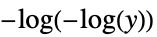
    "LogComplementLink"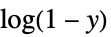
    "ComplementaryLogLogLink"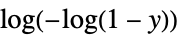
    "OddsPowerLink"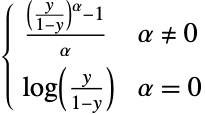
  • データの数え上げのための他の一般的なリンク関数
  • "NegativeBinomialLink"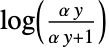
  • 正の実数値データのための他の一般的なリンク関数
  • "PowerLink"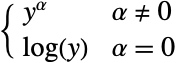
  • "OddsPowerLink"，"NegativeBinomialLink"，"PowerLink"については，LinkFunction->{linkname,"LinkParameter"->α}で追加的なパラメータ α を与えることができる．パラメータ α は"OddsPowerLink"と"PowerLink"については任意の実数値，"NegativeBinomialLink"については任意の正の値でよい．
  • LinkFunction->gでは，g はモデルの応答領域において正の値で可逆である任意の純関数でよい．

例題

例  (1)

正準Logリンクを持つポアソン(Poisson)モデルをフィットする：

名前付きのリンクを使う：

シフトされたSqrtリンクに純関数を使う：

Wolfram Research (2008), LinkFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/LinkFunction.html.

テキスト

Wolfram Research (2008), LinkFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/LinkFunction.html.

CMS

Wolfram Language. 2008. "LinkFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LinkFunction.html.

APA

Wolfram Language. (2008). LinkFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LinkFunction.html

BibTeX

@misc{reference.wolfram_2024_linkfunction, author="Wolfram Research", title="{LinkFunction}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/LinkFunction.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_linkfunction, organization={Wolfram Research}, title={LinkFunction}, year={2008}, url={https://reference.wolfram.com/language/ref/LinkFunction.html}, note=[Accessed: 22-November-2024 ]}