MatrixSymbol
MatrixSymbol[a]
a という名前の行列を表す.
MatrixSymbol[a,{m,n}]
mn 行列を表す.
MatrixSymbol[a,{m,n},dom]
要素が領域 dom のものである行列を表す.
MatrixSymbol[a,{m,n},dom, sym]
対称性 sym の行列を表す.
詳細
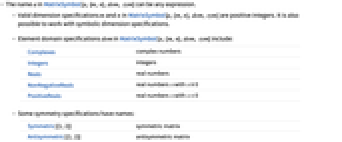
- MatrixSymbol[a,{m,n},dom, sym]の名前 a は任意の式でよい.
- MatrixSymbol[a,{m,n},dom, sym]における有効な次元指定 m および n は,正の整数である.記号による次元指定を使うこともできる.
- MatrixSymbol[a,{m,n},dom, sym]における要素領域の指定 dom には,以下が含まれる.
-
Complexes 複素数 Integers 整数 Reals 実数 NonNegativeReals 実数 x (x≥0) PositiveReals 実数 x (x>0) - 対称指定の中には名前があるものがある.
-
Symmetric[{1,2}] 対称行列 Antisymmetric[{1,2}] 非対称行列 - リストを扱う算術関数および多くの他の関数では,MatrixSymbolオブジェクトは他のリストの引数とは自動的には結合されない.
- 最適化関数,方程式のソルバ,Dは,MatrixSymbolオブジェクトがベクトル変数を表すことを認識する.
例題
すべて開くすべて閉じる例 (1)
アプリケーション (4)
ペア![]() のリストとして与えられたデータ
のリストとして与えられたデータ ![]() についての最小二乗解を導出する:
についての最小二乗解を導出する:
ポートフォリオ最適化問題の最適性の条件を,期待利益 ![]() ,標準偏差
,標準偏差 ![]() で求める:
で求める:
目的は,アセットの重みのベクトル ![]() がTotal[x]=1を満足するときに
がTotal[x]=1を満足するときに ![]() を最大にすることである.制約条件を使って
を最大にすることである.制約条件を使って ![]() を表すことができる.ここで,制約がないベクトル変数
を表すことができる.ここで,制約がないベクトル変数 ![]() は
は ![]() の最初の
の最初の ![]() 座標からなる:
座標からなる:
方程式 ![]() で表される線形回帰モデルの対数尤度関数の傾きを計算する.ここで,
で表される線形回帰モデルの対数尤度関数の傾きを計算する.ここで,![]() は正規分布に従う平均が0で分散が
は正規分布に従う平均が0で分散が ![]() の確率変数である:
の確率変数である:
テキスト
Wolfram Research (2024), MatrixSymbol, Wolfram言語関数, https://reference.wolfram.com/language/ref/MatrixSymbol.html.
CMS
Wolfram Language. 2024. "MatrixSymbol." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MatrixSymbol.html.
APA
Wolfram Language. (2024). MatrixSymbol. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MatrixSymbol.html