PositiveReals

PositiveReals

represents the domain of strictly positive real numbers.

Details

  • x∈PositiveReals evaluates immediately if x is a numeric quantity.
  • Simplify[expr∈PositiveReals,assum] can be used to try to determine whether an expression corresponds to a positive real number under the given assumptions.
  • (x1|x2|…)∈PositiveReals and {x1,x2,…}∈PositiveReals test whether all xi are positive real numbers.
  • PositiveReals is output in StandardForm and TraditionalForm as 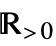. This typeset form can be input using preals.

Examples

open allclose all

Basic Examples  (3)

is a positive real number:

If is a real number, then is a positive real number:

Find positive real solutions of an equation:

Scope  (4)

Test if a numeric quantity is positive:

Make domain membership assumptions:

Specify the default domain over which a function should work:

Test whether several numbers are positive reals:

If any number is explicitly not a positive number, the result is False:

Applications  (1)

Testing membership in the positive reals is a fast way to verify positivity of a large list:

Properties & Relations  (4)

Membership in PositiveReals is equivalent to membership in Reals along with positivity:

PositiveReals contains PositiveRationals and PositiveIntegers:

PositiveReals is contained in Complexes:

PositiveReals is disjoint from NonPositiveReals and NegativeReals:

Wolfram Research (2019), PositiveReals, Wolfram Language function, https://reference.wolfram.com/language/ref/PositiveReals.html.

Text

Wolfram Research (2019), PositiveReals, Wolfram Language function, https://reference.wolfram.com/language/ref/PositiveReals.html.

CMS

Wolfram Language. 2019. "PositiveReals." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PositiveReals.html.

APA

Wolfram Language. (2019). PositiveReals. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PositiveReals.html

BibTeX

@misc{reference.wolfram_2024_positivereals, author="Wolfram Research", title="{PositiveReals}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/PositiveReals.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_positivereals, organization={Wolfram Research}, title={PositiveReals}, year={2019}, url={https://reference.wolfram.com/language/ref/PositiveReals.html}, note=[Accessed: 22-December-2024 ]}