MersennePrimeExponentQ

MersennePrimeExponentQ[n]

returns True if n is a Mersenne prime exponent, and False otherwise.

Details

  • MersennePrimeExponentQ is typically used to test whether an integer is a Mersenne prime exponent.
  • A positive integer n is a Mersenne prime exponent if the Mersenne number 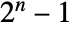is prime.
  • MersennePrimeExponentQ[n] returns False unless n is manifestly a Mersenne prime exponent.

Examples

open allclose all

Basic Examples  (2)

Test whether a number is a Mersenne prime exponent:

The number is not a Mersenne prime exponent:

Scope  (3)

MersennePrimeExponentQ works over integers:

Negative integers are not Mersenne prime exponents:

Noninteger numbers are not Mersenne prime exponents:

Applications  (8)

Basic Applications  (3)

Highlight Mersenne prime exponents:

Generate random Mersenne prime exponents:

Digits of a Mersenne prime :

Special Sequences  (2)

Recognize Mersenne numbers, numbers of the form :

The number is a Mersenne number; is not:

Recognize Gaussian Mersenne primes, prime numbers n such that is a Gaussian prime:

Number Theory  (3)

A trinomial whose order is a Mersenne prime exponent is primitive modulo if and only if it is irreducible:

If p is a Mersenne prime exponent, then is a perfect number:

Every even perfect number has the form , where p is a Mersenne prime exponent:

Check that in the representation above p is 5:

Properties & Relations  (10)

Mersenne prime exponents are prime numbers:

Composite numbers cannot be MersennePrimeExponents:

The only even Mersenne prime exponent is :

MersennePrimeExponent gives Mersenne prime exponent:

is a Mersenne prime, where p is a Mersenne prime exponent:

If p is a Mersenne prime exponent, then is a perfect number:

Every even perfect number has the form , where p is a Mersenne prime exponent:

Check that in the representation above p is 5:

Triangular numbers of Mersenne primes are perfect numbers:

Hexagonal numbers related to Mersenne prime exponents are perfect numbers:

Find Mersenne prime exponents:

Possible Issues  (1)

Expressions that represent Mersenne prime exponents but do not evaluate explicitly will give False:

It is necessary to use symbolic simplification first:

Neat Examples  (1)

The minor planet 8191 Mersenne is named after Marin Mersenne:

The number is a Mersenne prime:

Wolfram Research (2016), MersennePrimeExponentQ, Wolfram Language function, https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html.

Text

Wolfram Research (2016), MersennePrimeExponentQ, Wolfram Language function, https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html.

CMS

Wolfram Language. 2016. "MersennePrimeExponentQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html.

APA

Wolfram Language. (2016). MersennePrimeExponentQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html

BibTeX

@misc{reference.wolfram_2024_mersenneprimeexponentq, author="Wolfram Research", title="{MersennePrimeExponentQ}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mersenneprimeexponentq, organization={Wolfram Research}, title={MersennePrimeExponentQ}, year={2016}, url={https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html}, note=[Accessed: 18-November-2024 ]}