MersennePrimeExponentQ

MersennePrimeExponentQ[n]

n がメルセンヌ(Mersenne)素数指数の場合はTrueを，それ以外の場合はFalseを返す．

詳細

  • MersennePrimeExponentQは，ある整数がメルセンヌ素数指数かどうかをテストするためにしばしば使われる．
  • メルセンヌ数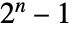が素数であれば，正の整数 n はメルセンヌ素数指数である．
  • n が明らかにメルセンヌ素数指数でなければ，MersennePrimeExponentQ[n]はFalseを返す．

例題

すべて開くすべて閉じる

例  (2)

ある数がメルセンヌ素数指数かどうかを判定する：

はメルセンヌ素数指数ではない：

スコープ  (3)

MersennePrimeExponentQは整数に使うことができる：

負の整数はメルセンヌ素数指数ではない：

整数以外の数はメルセンヌ素数指数ではない：

アプリケーション  (8)

基本的なアプリケーション  (3)

メルセンヌ素数指数をハイライトする：

ランダムなメルセンヌ素数指数を生成する：

メルセンヌ素数 の各桁の数字：

特殊数列  (2)

メルセンヌ素数（ という形の数）を認識する：

数はメルセンヌ素数だがはそうではない：

ガウスメルセンヌ素数（がガウス素数となるような素数 n）を認識する：

整数論  (3)

次数がメルセンヌ素数指数である三項式は，この式が簡約可能なときかつそのときに限りを法として原始的である：

p がメルセンヌ素数指数なら，は完全数である：

偶数の完全数はどれも（p はメルセンヌ素数指数）の形をしている：

上記の表現では p が5であることを確かめる：

特性と関係  (10)

メルセンヌ素数指数は素数である：

合成数がMersennePrimeExponentであることはない：

唯一の偶メルセンヌ素数指数はである：

MersennePrimeExponentは 番目のメルセンヌ素数指数を与える：

はメルセンヌ素数である．ただし，p はメルセンヌ素数指数である：

p がメルセンヌ素数指数であるなら，は完全数である：

すべての偶数の完全数がの形を持つ．この中の p はメルセンヌ素数指数である：

上記の表現で p が5であることを確かめる：

メルセンヌ素数の三角数は完全数である：

メルセンヌ素数指数に関連付けられた六角数は完全数である：

メルセンヌ素数指数を求める：

考えられる問題  (1)

明示的に評価できない式は，メルセンヌ素数指数を表す場合でもFalseを返す：

まず記号的な簡約を行うことが必要である：

おもしろい例題  (1)

小惑星8191メルセンヌはマラン メルセンヌ(Marin Mersenne)に因んで命名された：

はメルセンヌ素数である：

Wolfram Research (2016), MersennePrimeExponentQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html.

テキスト

Wolfram Research (2016), MersennePrimeExponentQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html.

CMS

Wolfram Language. 2016. "MersennePrimeExponentQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html.

APA

Wolfram Language. (2016). MersennePrimeExponentQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html

BibTeX

@misc{reference.wolfram_2024_mersenneprimeexponentq, author="Wolfram Research", title="{MersennePrimeExponentQ}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mersenneprimeexponentq, organization={Wolfram Research}, title={MersennePrimeExponentQ}, year={2016}, url={https://reference.wolfram.com/language/ref/MersennePrimeExponentQ.html}, note=[Accessed: 18-November-2024 ]}